Twierdzenie sinusów

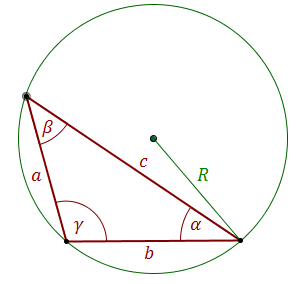
Twierdzenie sinusów

W dowolnym trójkącie stosunek długości dowolnego boku do sinusa kąta naprzeciw tego boku jest stały i równy długości średnicy okręgu opisanego na trójkącie. \[\frac{a}{\sin \alpha }=\frac{b}{\sin \beta }=\frac{c}{\sin \gamma }=2R\] gdzie \(R\) - to długość promienia okręgu opisanego na trójkącie