Trójkąt prostokątny 45° 45° 90°
Poziom podstawowy
Trójkąt prostokątny z kątem ostrym \(45^\circ \) możemy uzyskać w kwadracie po narysowaniu przekątnej.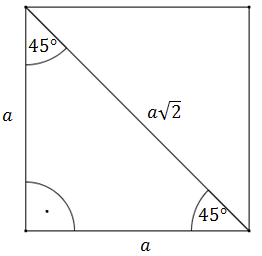 
Przekątna kwadratu o boku \(a\) ma długość \(a\sqrt{2}\).Rozważmy na oddzielnym rysunku sam trójkąt prostokątny:
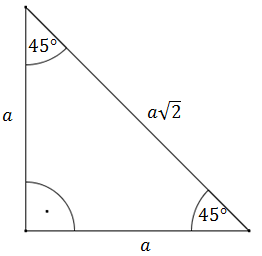Korzystając z definicji funkcji trygonometrycznych obliczamy: \[\begin{split}&\sin 45^\circ =\frac{a}{a\sqrt{2}}=\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}\\[10pt]&\cos 45^\circ =\frac{a}{a\sqrt{2}}=\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}\\[10pt]&\operatorname{tg} 45^\circ =\frac{a}{a}=1\\[10pt]&\operatorname{ctg} 45^\circ =\frac{a}{a}=1\\[10pt]\end{split}\] Oblicz długość odcinków \(x\text{ i }y\).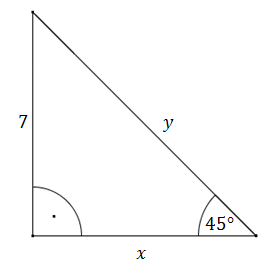 
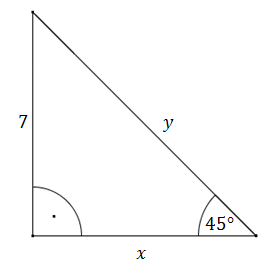
Na początku zauważmy, że \(x=7\), bo trójkąt jest prostokątny. Wiemy, że odcinek \(y\) jest "tak jakby" przekątną kwadratu o boku długości \(7\), zatem \(y=7\sqrt{2}\).
Teraz rozwiążemy ten przykład jeszcze raz, tylko przy wykorzystaniu funkcji trygonometrycznych.
Odcinek \(x\) możemy policzyć z tangensa: \[\begin{split}\operatorname{tg} 45^\circ &=\frac{7}{x}\\[10pt]1&=\frac{7}{x}\\[10pt]x&=7\end{split}\] Odcinek \(y\) obliczymy z sinusa: \[\begin{split}\sin 45^\circ&=\frac{7}{y}\\[10pt]\frac{\sqrt{2}}{2}&=\frac{7}{y}\\[10pt]\sqrt{2}y&=14\\[10pt]y&=\frac{14}{\sqrt{2}}\\[10pt]y&=\frac{14\sqrt{2}}{2}\\[10pt]y&=7\sqrt{2}\end{split}\]
Odcinek \(x\) możemy policzyć z tangensa: \[\begin{split}\operatorname{tg} 45^\circ &=\frac{7}{x}\\[10pt]1&=\frac{7}{x}\\[10pt]x&=7\end{split}\] Odcinek \(y\) obliczymy z sinusa: \[\begin{split}\sin 45^\circ&=\frac{7}{y}\\[10pt]\frac{\sqrt{2}}{2}&=\frac{7}{y}\\[10pt]\sqrt{2}y&=14\\[10pt]y&=\frac{14}{\sqrt{2}}\\[10pt]y&=\frac{14\sqrt{2}}{2}\\[10pt]y&=7\sqrt{2}\end{split}\]
Tematy nadrzędne i sąsiednie