Trójkąt Pascala
Poziom rozszerzony
W trójkącie Pascala liczby skrajne są jedynkami, a pozostałe liczby są sumą dwóch liczb znajdujących się nad nią: \[ 1\\ 1\quad 1\\ 1\quad 2\quad 1\\ 1\quad 3\quad 3 \quad 1\\ 1\quad 4\quad 6\quad 4\quad 1\\ 1\quad 5\quad\! 10\quad\!\! 10\quad\! 5\quad 1\\ 1\quad 6\quad\!\! 15\quad\! 20\quad\! 15\quad\!\! 6\quad 1\\ 1\quad 7\quad\! 21\quad\! 35\quad\!\! 35\quad\! 21\quad\! 7\quad 1\\ 1\quad 8\quad\! 28\quad\! 56\quad\! 70\quad\! 56\quad\! 28\quad\! 8\quad 1\\ .\ \ .\ \ .\ \ .\ \ .\ \ .\ \ .\ \ .\ \ .\ \ .\ \ .\ \ .\ \ .\ \ .\ \ .\ \ .\ \ . \] Kolejne wiersze trójkąta Pascala zawierają współczynniki liczbowe wzoru dwumianowego Newtona: \[(a+b)^n=\binom{n}{0}a^nb^0+\binom{n}{1}a^{n-1}b^1+\binom{n}{2}a^{n-2}b^2+...+\binom{n}{n-1}a^1b^{n-1}+\binom{n}{n}a^0b^n \] gdzie \(\binom{n}{k} \) - to symbol Newtona i jest obliczany ze wzoru: \[\binom{n}{k}=\frac{n!}{k!\cdot (n-k)!} \] Oto ilustracja na pierwszych wierszach trójkąta Pascala: 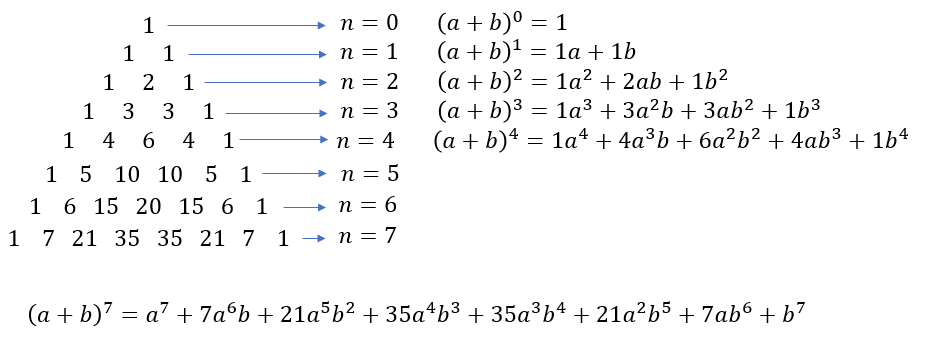
Tematy nadrzędne i sąsiednie