Środkowe w trójkącie
Poziom podstawowy
Definicja
Środkowa trójkąta to prosta zawierająca wierzchołek trójkąta i środek przeciwległego boku.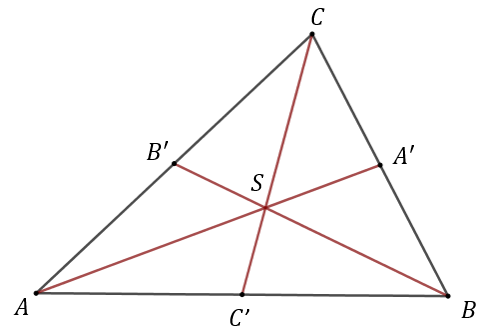
Twierdzenie
Środkowe trójkąta przecinają się w jednym punkcie (nazywanym środkiem ciężkości, środkiem masy lub barycentrum). Punkt ten dzieli każdą ze środkowych w stosunku \(2:1\), licząc od wierzchołka. \[\frac{|AS|}{|A'S|}=\frac{|BS|}{|B'S|}=\frac{|CS|}{|C'S|}=\frac{2}{1}\] Dowód:
Punkty \(A'\), \(B'\) oraz \(C'\) to środki boków trójkąta.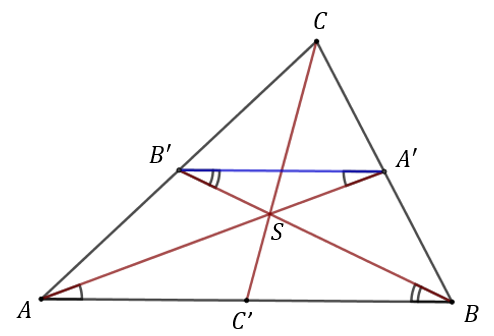
Z tego, że \(A'\) i \(B'\) to środki boków, mamy równość: \[\frac{|CB'|}{|CA|}=\frac{|CA'|}{|CB|}=\frac{1}{2}\] Zatem z twierdzenia odwrotnego do twierdzenia Talesa odcinek \(A'B'\) jest równoległy \(AB\).
Zatem mamy podobieństwo trójkątów: \[\triangle ABS\sim \triangle A'B'S\] ze skalą podobieństwa równą: \[\frac{|AB|}{|A'B'|}=\frac{2}{1}=2\] Zatem z podobieństwa mamy: \(|BS| : |SB'| = 2 : 1\) oraz \(|AS| : |SA'| = 2 : 1\).\(_{c.n.d.}\)
Punkty \(A'\), \(B'\) oraz \(C'\) to środki boków trójkąta.
Z tego, że \(A'\) i \(B'\) to środki boków, mamy równość: \[\frac{|CB'|}{|CA|}=\frac{|CA'|}{|CB|}=\frac{1}{2}\] Zatem z twierdzenia odwrotnego do twierdzenia Talesa odcinek \(A'B'\) jest równoległy \(AB\).Zatem mamy podobieństwo trójkątów: \[\triangle ABS\sim \triangle A'B'S\] ze skalą podobieństwa równą: \[\frac{|AB|}{|A'B'|}=\frac{2}{1}=2\] Zatem z podobieństwa mamy: \(|BS| : |SB'| = 2 : 1\) oraz \(|AS| : |SA'| = 2 : 1\).\(_{c.n.d.}\)
Analogicznie można wykazać, że: \(|CS| : |SC'| = 2 : 1\). Wystarczy wziąć np. odcinek \(B'C'\) i trójkąty podobne \(SBC\) oraz \(SB'C'\).
W trójkącie \(ABC\) zaznaczono środkową \(CD\). 
Środkowa \(CD\) dzieli ten trójkąt na dwa trójkąty o równych polach.
Środkowa \(CD\) dzieli ten trójkąt na dwa trójkąty o równych polach. Uzasadnienie:
Punkt \(D\) jest środkiem boku \(AB\), zatem \(|AD|=|BD|\).
Zatem trójkąty \(ADC\) i \(DBC\) i mają podstawy równej długości i wspólną wysokość \(h\), więc mają równe pola.
Punkt \(D\) jest środkiem boku \(AB\), zatem \(|AD|=|BD|\).
Zatem trójkąty \(ADC\) i \(DBC\) i mają podstawy równej długości i wspólną wysokość \(h\), więc mają równe pola.
Zaznaczmy na środkowej \(CD\) dowolny punkt \(P\).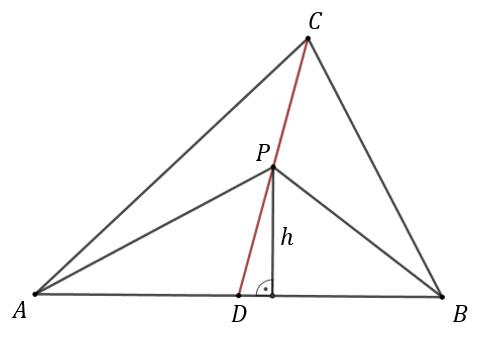 
Wówczas pola trójkątów \(ADP\) i \(DBP\) są równe.
Wówczas pola trójkątów \(ADP\) i \(DBP\) są równe. Wynika to z tego, że oba trójkąty mają podstawy równej długości i wspólną wysokość.
Twierdzenie o współrzędnych punktu ciężkości trójkąta
Jeżeli wierzchołki trójkąta mają współrzędne \(A=\left(a_1, a_2\right), B=\left(b_1, b_2\right), C=\left(c_1, c_2\right)\), to środek ciężkości \(S\) tego trójkąta ma współrzędne: \[S=\left(\frac{a_1+b_1+c_1}{3}, \frac{a_2+b_2+c_2}{3}\right)\]Współrzędne wierzchołków trójkąta \(ABC\) wynoszą \(A=(1,2), B=(3,4), C=(5,-3)\). Punkt \(S\) jest środkiem ciężkości tego trójkąta. Wyznacz odległość punktu \(S\) od wierzchołka \(A\).
Wyznaczamy współrzędne środka ciężkości: \[S=\left(\frac{1+3+5}{3}, \frac{2+4-3}{3}\right)=\left(\frac{9}{3}, \frac{3}{3}\right)=(3,1)\] Obliczamy długość odcinka \(AS\): \[|AS|=\sqrt{(3-1)^2+(1-2)^2}=\sqrt{2^2+(-1)^2}=\sqrt{5}\]
Eksperyment praktyczny
Aby sprawdzić jak działa środek ciężkości w trójkącie, możesz wykonać następujące doświadczenie:- Narysuj na sztywnym kartonie dowolny trójkąt.
- Wyznacz punkt przecięcia dwóch środkowych tego trójkąta (wyznacz wcześniej dokładnie środki boków).
- Wytnij narysowany trójkąt.
- Spróbuj ustawić ten trójkąt na jakimś czubku (np. ołówka), tak aby czubek podpierał trójkąt w punkcie przecięcia środkowych.
Dany jest kwadrat \(A B C D\) o boku długości \(a\). Punkt \(E\) jest środkiem boku \(C D\). Przekątna \(B D\) dzieli trójkąt \(A C E\) na dwie figury: \(A G F\) oraz \(C E F G\) (zobacz rysunek). 
Oblicz pola figur \(AGF\) oraz \(CEFG\). Zapisz obliczenia.
Tematy nadrzędne i sąsiednie