Schemat Hornera
Poziom podstawowy
Schemat Hornera wykorzystujemy do dzielenia wielomianu przez dwumian liniowy.Cała metoda jest podobna do dzielenia pisemnego wielomianów.
Podziel wielomian \(w(x)=3x^4-2x^2-5+x\) przez dwumian \(x+2\).
Zapisujemy wielomian \(w(x)\) w uporządkowany sposób, uwzględniając również jednomiany ze współczynnikiem zero: \[w(x)=3x^4+0\cdot x^3-2x^2+x-5\] Przygotowujemy tabelkę składającą się z dwóch wierszy:
Teraz zaczynamy dzielić wielomiany.
Współczynniki wielomianu, który będzie wynikiem dzielenia, będziemy zapisywali w pozostałych miejscach drugiego rzędu.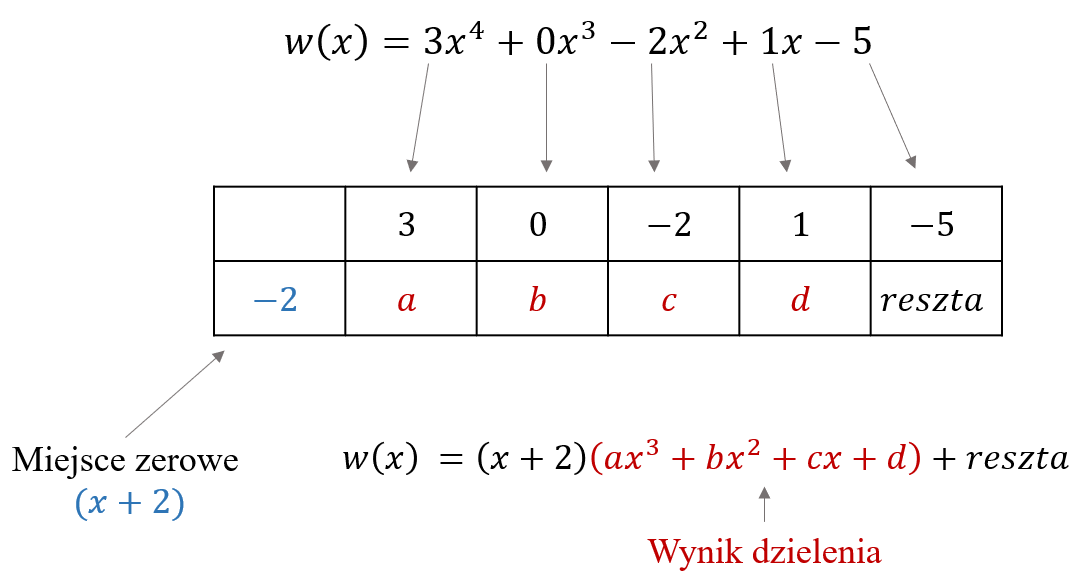 Teraz pokażemy jak wyliczyć szukane współczynniki \(a, b, c, d\) i resztę.
Teraz pokażemy jak wyliczyć szukane współczynniki \(a, b, c, d\) i resztę.
Zatem: \[w(x)=(x+2)(3x^3-6x^2+10x-19)+33\]
- W pierwszym wierszu wypisujemy kolejno wszystkie współczynniki wielomianu \(w(x)\) uwzględniając również te zerowe (pierwsze pole zostawiamy puste - nie będzie do niczego wykorzystane).
- W drugim wierszu w pierwszym polu wpisujemy miejsce zerowe dwumianu przez który dzielimy (w tym przypadku jest to liczba \((-2)\) - miejsce zerowe dwumianu \(x+2\)).
| \(3\) | \(0\) | \(-2\) | \(1\) | \(-5\) | |
| \(-2\) |
Współczynniki wielomianu, który będzie wynikiem dzielenia, będziemy zapisywali w pozostałych miejscach drugiego rzędu.
 Teraz pokażemy jak wyliczyć szukane współczynniki \(a, b, c, d\) i resztę.
Teraz pokażemy jak wyliczyć szukane współczynniki \(a, b, c, d\) i resztę. - Pierwszy współczynnik \(a\), to liczba z wiersza powyżej, czyli \(a=3\).
- Drugi współczynnik \(b\), to suma: (iloczyn współczynnika wyliczonego w poprzednim kroku, czyli \(3)\) i miejsca zerowego dwumianu przez który dzielimy, czyli (\(-2)\)) + (liczba z wiersza powyżej). Zatem: \[b=a\cdot (-2)+0=3\cdot (-2)+0=-6\]
- Każdy kolejny współczynnik wyliczamy na takiej samej zasadzie jak drugi, czyli: \[\begin{split} &c=b\cdot (-2)+(-2)=(-6)\cdot (-2)+(-2)=10\\[6pt] &d=c\cdot (-2)+1=10\cdot (-2)+1=-19\\[6pt] &\text{reszta}\ = d\cdot (-2)+(-5)=(-19)\cdot (-2)+(-5)=33 \end{split}\]
| \(3\) | \(0\) | \(-2\) | \(1\) | \(-5\) | |
| \(-2\) | \(3\) | \(-6\) | \(10\) | \(-19\) | \(33\) |
W tym nagraniu wideo pokazuję na konkretnych przykładach, jak należy stosować Schemat Hornera do podzielenia jednego wielomianu przez dwumian.
Tematy nadrzędne i sąsiednie