Dzielenie wielomianów
Poziom podstawowy
Wykonaj dzielenie pisemne wielomianów: \((3x^3-5x^2-2x):(x^2-2x)\).
Całe działanie wygląda tak: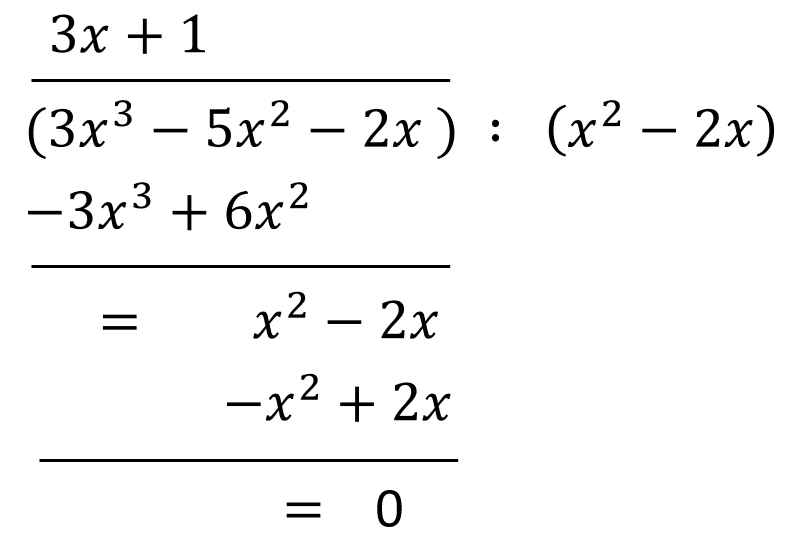 
Wielomiany podzieliły się bez reszty.
Zatem dzieląc wielomian \(3x^3-5x^2-2x\) przez wielomian \(x^2-2x\) otrzymujemy wielomian \(3x+1\).
Możemy zapisać: \[3x^3-5x^2-2x=(x^2-2x)\cdot (3x+1)\] Całę metodę wykonania tego rachunku przedstawiam poniżej:
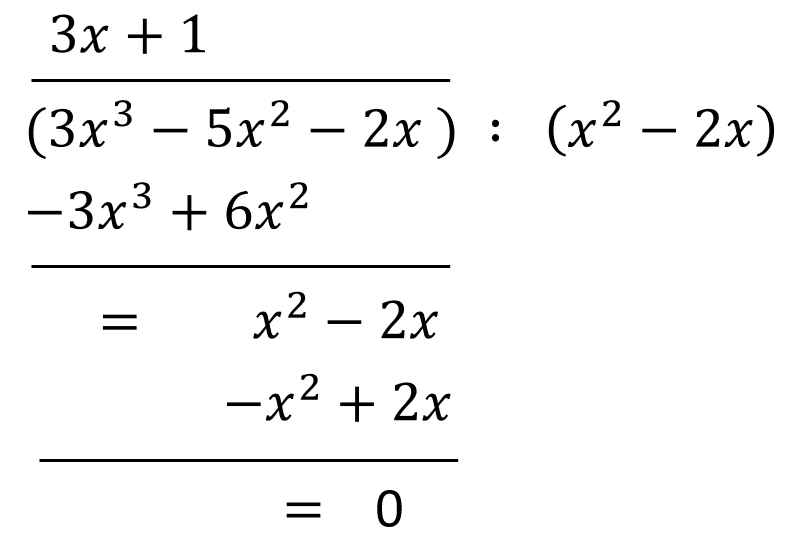Wielomiany podzieliły się bez reszty.Zatem dzieląc wielomian \(3x^3-5x^2-2x\) przez wielomian \(x^2-2x\) otrzymujemy wielomian \(3x+1\).
Możemy zapisać: \[3x^3-5x^2-2x=(x^2-2x)\cdot (3x+1)\] Całę metodę wykonania tego rachunku przedstawiam poniżej:
Wykonaj dzielenie pisemne wielomianów: \((5x^3-2x^2+x-4):(x^2-3)\).
Całe działanie wygląda tak: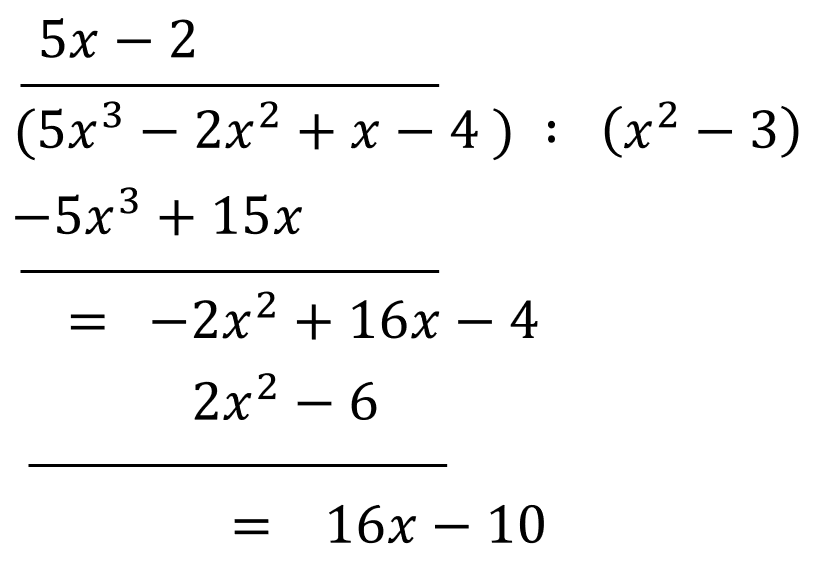 
Zatem dzieląc wielomian \(5x^3-2x^2+x-4\) przez wielomian \(x^2-3\) otrzymujemy wielomian \(5x-2\) i jeszcze resztę \(16x-10\).
Możemy zapisać:
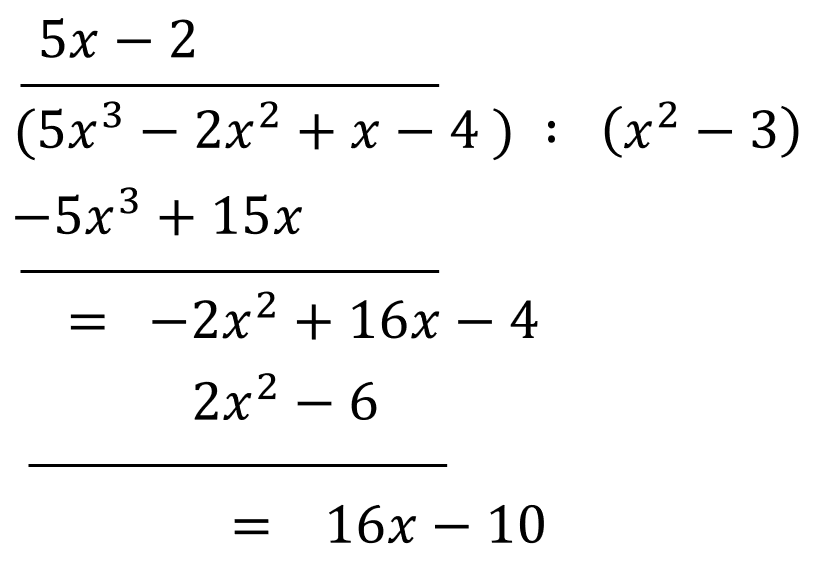Zatem dzieląc wielomian \(5x^3-2x^2+x-4\) przez wielomian \(x^2-3\) otrzymujemy wielomian \(5x-2\) i jeszcze resztę \(16x-10\).Możemy zapisać:
\[5x^3-2x^2+x-4=(x^2-3)\cdot (5x-2) + 16x-10\]
Lekcja 1. Dzielenie pisemne wielomianów w pamięci
W tej lekcji pokazuję jak szybko znajdować postać iloczynową wielomianu na przykładach:
- \(x^3+x^2-16 x+20=0\)
- \(2 x^3+5 x^2-x-6=0\)
Zadanie 1.
Wykonaj dzielenie poniższych wielomianów:
\(\frac{x^4}{x^3}\)
\(\frac{3x^5}{x^2}\)
\(\frac{17x^3}{x^2}\)
Zadanie 2.
Wykonaj pisemne dzielenie liczb \(86735 : 5\).
Zadanie 3.
Wykonaj dzielenie wielomianów \((x^2 + 4x - 5) : (x - 1)\).
Zadanie 4.
Wykonaj dzielenie wielomianów \((6x^2 - x - 2) : (2x + 1)\).
Zadanie 5.
Wykonaj dzielenie wielomianów \((x^3 + 9x^2 - 20x - 4) : (x - 2)\)
Zadanie 6.
Wykonaj dzielenie wielomianów \((2x^7 - 10x^5 - 6x^4 + 2) : (2x^3 - 6)\) .