Różne zadania z funkcji wykładniczej
Napisz wzór funkcji wykładniczej f(x) = ax, gdzie a > 0, wiedząc że do jej wykresu należy punkt A(3, 1/8).
Rozwiązanie PDF
- Naszkicuj wykres funkcji g(x) = f(x + 2) - 1.
- Oblicz miejsca zerowe funkcji g(x).
- Dla jakich argumentów funkcja g(x) przyjmuje wartości ujemne?
Rozwiązanie PDF Na rysunku przedstawiony jest wykres funkcji f(x) = (2/3)x - 1, gdzie a > 0, \(x\epsilon \mathbb{R} \).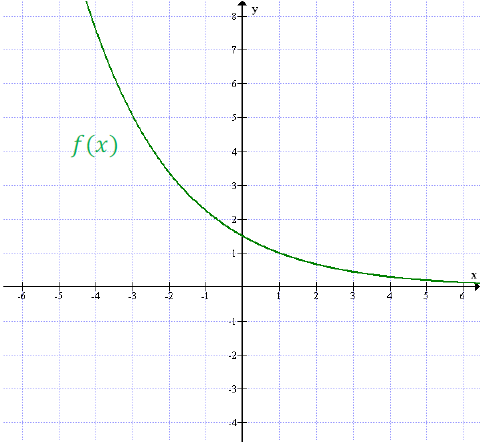 
Rozwiązanie PDF
- Oblicz wartość funkcji dla argumentu 1/2.
- Oblicz argument dla którego wartość funkcji wynosi 16/81.
- Dla jakich argumentów wartości funkcji f są większe od \(2\frac{1}{4}\).
- Napisz wzór i naszkicuj wykres funkcji g(x) = f(-x) - 3.
Rozwiązanie PDF 
przyjmuje wartości większe niż funkcja 
Wyznacz wartość parametru k, jeżeli wiadomo, że dla argumentu x = 1 funkcje 
przyjmują tą samą wartość.
Rozwiązanie PDF
przyjmują tą samą wartość. Rozwiązanie PDF Naszkicuj wykres funkcji: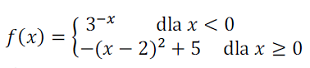 
Na podstawie wykresu funkcji f ustal liczbę rozwiązań równania f(x) = k, gdzie k?R, w zależności od wartości parametru k.
Rozwiązanie PDF
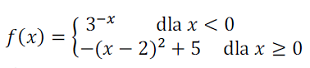Na podstawie wykresu funkcji f ustal liczbę rozwiązań równania f(x) = k, gdzie k?R, w zależności od wartości parametru k. Rozwiązanie PDF Wykresy funkcji 
mają z osią OY ten sam punkt wspólny A. Oblicz k i podaj współrzędne punktu A.
Rozwiązanie PDF
mają z osią OY ten sam punkt wspólny A. Oblicz k i podaj współrzędne punktu A. Rozwiązanie PDF Funkcje 
mają to samo miejsce zerowe. Oblicz wspólne miejsce zerowe obu funkcji oraz wartość parametru p.
Rozwiązanie PDF
mają to samo miejsce zerowe. Oblicz wspólne miejsce zerowe obu funkcji oraz wartość parametru p. Rozwiązanie PDF Zadanie 1.
Do wykresu funkcji, określonej dla wszystkich liczb rzeczywistych wzorem \( y=-2^{x-2} \), należy punkt
A.\(A=(1,-2) \)
B.\(B=(2,-1) \)
C.\(C=(1,\frac{1}{2}) \)
D.\(D=(4,4) \)
Zadanie 2.
Dane są dwie funkcje określone dla wszystkich liczb rzeczywistych \( x \) wzorami \( f(x)=-5x+1 \) oraz \(g(x) = 5^x\). Liczba punktów wspólnych wykresów tych funkcji wynosi
A.\(3\)
B.\(2\)
C.\(1\)
D.\(0\)
Zadanie 3.
Zbiorem wartości funkcji \(f\) określonej wzorem \(f(x)=3^{x+2}-3\) jest zbiór
A.\( (-2;\infty ) \)
B.\( (-3;-2) \)
C.\( (3;\infty ) \)
D.\( (-3;\infty ) \)
Zadanie 4.
Funkcja wykładnicza określona wzorem \(f(x)=3^x\) przyjmuje wartość \(6\) dla argumentu
A.\( x=2 \)
B.\( x=\log_{3}2 \)
C.\( x=\log_{3}6 \)
D.\( x=\log_{6}3 \)