Romb

Drukuj

Poziom podstawowy

Romb - to czworokąt, który ma wszystkie boki równej długości. Przekątne rombu przecinają się pod kątem prostym.

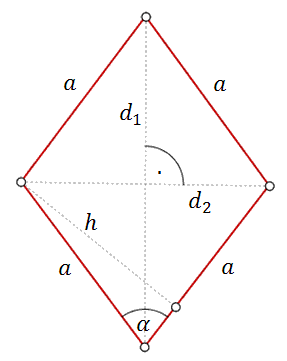
Wzór na obwód rombu: \[Ob=4a\]

Wzory na pole rombu: \[P=a\cdot h\\[6pt] P=a^2\sin \alpha \\[6pt] P=\frac{d_1\cdot d_2}{2}\]

W rombie bok i krótsza przekątna mają taką samą długość, równą \(a\). Wówczas dłuższa przekątna ma długość:

A.\( a\sqrt{2} \)

B.\( a\sqrt{3} \)

C.\( 2a \)

D.\( \frac{a\sqrt{3}}{2} \)

Bok rombu ma długość \(8\), a kąt ostry ma miarę \(60^\circ \). Wysokość tego rombu jest więc równa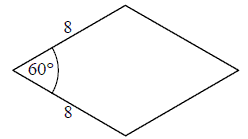

A.\( 2\sqrt{3} \)

B.\( 4\sqrt{3} \)

C.\( 6\sqrt{3} \)

D.\( 8\sqrt{3} \)

Dany jest romb o boku długości \(4\) i kącie ostrym \(60^\circ\). Pole tego rombu jest równe

A.\( 16\sqrt{3} \)

B.\( 16 \)

C.\( 8\sqrt{3} \)

D.\( 8 \)

Wysokość rombu o boku długości \(6\) i kącie ostrym \(60^\circ\) jest równa

A.\( 3\sqrt{3} \)

B.\( 3 \)

C.\( 6\sqrt{3} \)

D.\( 6 \)

Dany jest romb, którego kąt ostry ma miarę \(45^\circ\), a jego pole jest równe \(50\sqrt{2}\). Oblicz wysokość tego rombu.

\(h=5\sqrt{2}\)

Pole rombu o obwodzie \(8\) jest równe \(1\). Kąt ostry tego rombu ma miarę \(\alpha \). Wtedy

A.\( 29^\circ \lt \alpha \lt 30^\circ \)

B.\( 14^\circ \lt \alpha \lt 15^\circ \)

C.\( 75^\circ \lt \alpha \lt 76^\circ \)

D.\( 60^\circ \lt \alpha \lt 61^\circ \)

Pole rombu o boku \(6\) i kącie rozwartym \(150^\circ \) jest równe

A.\( 18\sqrt{2} \)

B.\( 18 \)

C.\( 36\sqrt{2} \)

D.\( 36 \)