Przekształcenia wykresu funkcji
Poziom rozszerzony
Naszkicuj wykres funkcji \(f(x)=\left|\frac{1}{x}\right|\).
Najpierw szkicujemy wykres funkcji \(y=\frac{1}{x}\), a następnie \(f(x)=\left|\frac{1}{x}\right|\):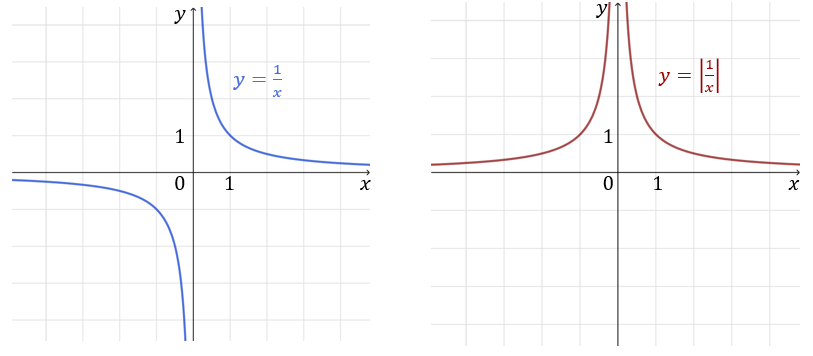 
Naszkicuj wykres funkcji \(f(x)=-\left|\frac{1}{x}\right|+3\).
Najpierw szkicujemy wykres funkcji \(y=-\left|\frac{1}{x}\right|\), który jest odbiciem wykresu funkcji \(y=\left|\frac{1}{x}\right|\) względem osi \(x\)-ów.
Następnie przesuwamy wykres o wektor \([0, 3]\) i otrzymujemy szukany wykres funkcji \(f(x)\):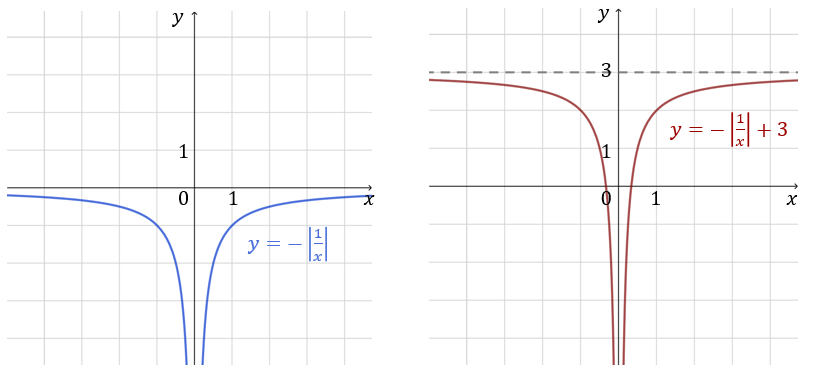
Następnie przesuwamy wykres o wektor \([0, 3]\) i otrzymujemy szukany wykres funkcji \(f(x)\):
Naszkicuj wykres funkcji \(f(x)=\left|\frac{1}{x}-2\right|\) i określ jej zbiór wartości. Podaj liczbę rozwiązań równania \(\left|\frac{1}{x}-2\right|=m\) w zależności od parametru \(m\).
Najpierw szkicujemy wykres funkcji \(y=\frac{1}{x}-2\) (jako przesunięcie wykresu \(y=\frac{1}{x}\) o \(2\) jednostki w dół), a następnie \(f(x)=\left|\frac{1}{x}-2\right|\):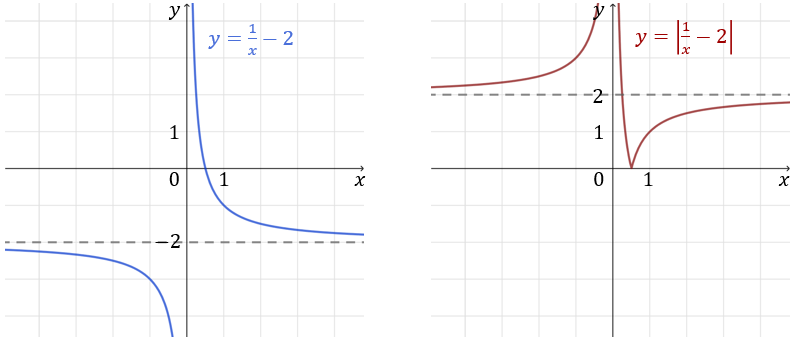 
Z wykresu odczytujemy zbiór wartości: \(\langle 0, +\infty )\).
Liczba rozwiązań równania \(\left|\frac{1}{x}-2\right|=m\) w zależności od parametru \(m\) jest równa liczbie punktów przecięcia prostej \(y=m\) z wykresem funkcji \(y=\left|\frac{1}{x}-2\right|\):
Z wykresu odczytujemy zbiór wartości: \(\langle 0, +\infty )\).Liczba rozwiązań równania \(\left|\frac{1}{x}-2\right|=m\) w zależności od parametru \(m\) jest równa liczbie punktów przecięcia prostej \(y=m\) z wykresem funkcji \(y=\left|\frac{1}{x}-2\right|\):
- \(0\) rozwiązań dla \(m\lt 0\),
- \(1\) rozwiązanie dla \(m\in \{0, 2\}\),
- \(2\) rozwiązania dla \(m\in (0; 2)\cup (2; +\infty )\).
Naszkicuj wykres funkcji \(f(x)=-\left|\frac{1}{x}-2\right|+1\) i określ jej zbiór wartości. Podaj liczbę rozwiązań równania \(-\left|\frac{1}{x}-2\right|+1=m\) w zależności od parametru \(m\).
Najpierw szkicujemy wykres funkcji \(y=\left|\frac{1}{x}-2\right|\) (tak jak w poprzednim przykładzie).
Następnie odbijamy wykres względem osi \(x\)-ów, otrzymując wykres funkcji \(y=-\left|\frac{1}{x}-2\right|\)
Teraz przesuwamy wykres o wektor \([0,1]\) i otrzymujemy szukany wykres funkcji \(y=-\left|\frac{1}{x}-2\right|+1\):
Z wykresu odczytujemy zbiór wartości: \((-\infty; 1\rangle )\).
Liczba rozwiązań równania \(-\left|\frac{1}{x}-2\right|+1=m\) w zależności od parametru \(m\) jest równa liczbie punktów przecięcia prostej \(y=m\) z wykresem funkcji \(y=-\left|\frac{1}{x}-2\right|+1\):
Następnie odbijamy wykres względem osi \(x\)-ów, otrzymując wykres funkcji \(y=-\left|\frac{1}{x}-2\right|\)
Teraz przesuwamy wykres o wektor \([0,1]\) i otrzymujemy szukany wykres funkcji \(y=-\left|\frac{1}{x}-2\right|+1\):
Z wykresu odczytujemy zbiór wartości: \((-\infty; 1\rangle )\).Liczba rozwiązań równania \(-\left|\frac{1}{x}-2\right|+1=m\) w zależności od parametru \(m\) jest równa liczbie punktów przecięcia prostej \(y=m\) z wykresem funkcji \(y=-\left|\frac{1}{x}-2\right|+1\):
- \(0\) rozwiązań dla \(m\gt 1\),
- \(1\) rozwiązanie dla \(m\in \{-1, 1\}\),
- \(2\) rozwiązania dla \(m\in (-1; 1)\cup (-\infty;-1)\).
Naszkicuj wykres funkcji \(f(x)=\frac{1}{|x-2|}\). Określ jej dziedzinę i zbiór wartości.
Wykres funkcji \(f(x)=\frac{1}{|x-2|}\) otrzymujemy przez przesunięcie wykresu funkcji \(y=\frac{1}{|x|}\) o wektor \([2,0]\):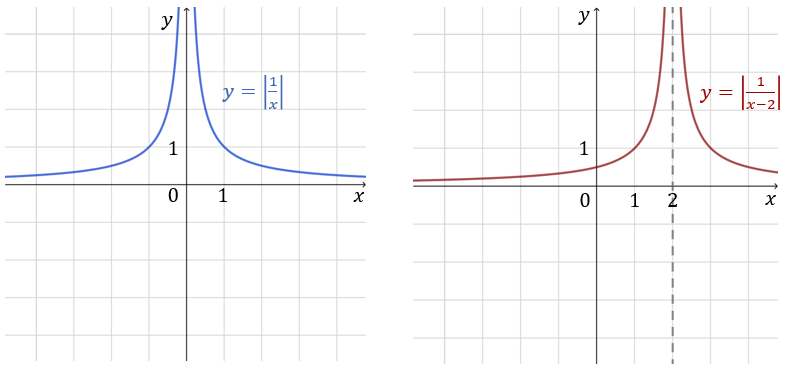 
Dziedziną funkcji \(f(x)=\frac{1}{|x-2|}\) jest \(x\in \mathbb{R} \backslash \{2\}\).
Zbiorem wartości jest przedział: \((0; +\infty )\).
Dziedziną funkcji \(f(x)=\frac{1}{|x-2|}\) jest \(x\in \mathbb{R} \backslash \{2\}\).Zbiorem wartości jest przedział: \((0; +\infty )\).
Naszkicuj wykres funkcji \(f(x)=\frac{1}{|x|-2}\). Określ jej dziedzinę i zbiór wartości.
Wykresu funkcji \(f(x)=\frac{1}{|x|-2}\) nie da się określić przez przesunięcie wykresu funkcji \(y=\frac{1}{|x|}\) o wektor.
Należy zauważyć, że wykres funkcji \(f(x)\) jest symetryczny względem osi \(y\)-ów, bo dla dowolnego \(x\) zachodzi: \[f(-x)=\frac{1}{|-x|-2}=\frac{1}{|x|-2}=f(x)\] Wystarczy zatem naszkicować jej wykres dla \(x\ge 0\) i następnie odbić go symetrycznie na ujemną dziedzinę.
Wzór funkcji \(f(x)\) dla \(x\ge 0\) jest następujący: \(f(x)=\frac{1}{x-2}\). Szkicujemy go i odbijamy symetrycznie: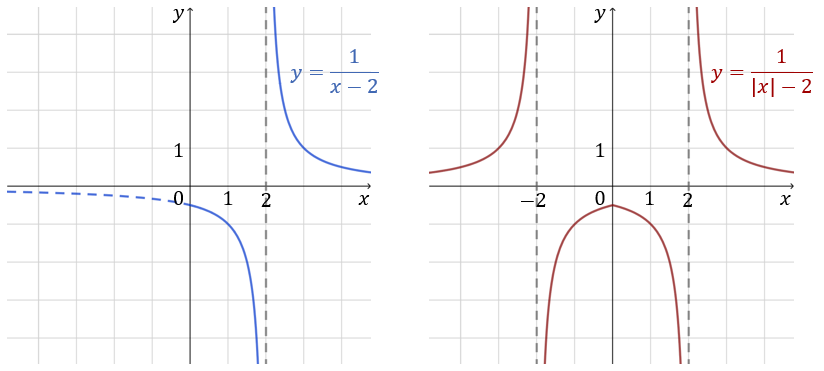
Dziedziną funkcji \(f(x)=\frac{1}{|x|-2}\) jest \(x\in \mathbb{R} \backslash \{-2, 2\}\).
Do określenia zbioru wartości potrzebujemy znać punkt przecięcia z osią \(y\)-ów: \[f(0)=\frac{1}{0-2}=-\frac{1}{2}\] Zatem zbiór wartości to: \(\left(-\infty; -\frac{1}{2}\right)\cup (0; +\infty )\).
Należy zauważyć, że wykres funkcji \(f(x)\) jest symetryczny względem osi \(y\)-ów, bo dla dowolnego \(x\) zachodzi: \[f(-x)=\frac{1}{|-x|-2}=\frac{1}{|x|-2}=f(x)\] Wystarczy zatem naszkicować jej wykres dla \(x\ge 0\) i następnie odbić go symetrycznie na ujemną dziedzinę.
Wzór funkcji \(f(x)\) dla \(x\ge 0\) jest następujący: \(f(x)=\frac{1}{x-2}\). Szkicujemy go i odbijamy symetrycznie:
Dziedziną funkcji \(f(x)=\frac{1}{|x|-2}\) jest \(x\in \mathbb{R} \backslash \{-2, 2\}\).Do określenia zbioru wartości potrzebujemy znać punkt przecięcia z osią \(y\)-ów: \[f(0)=\frac{1}{0-2}=-\frac{1}{2}\] Zatem zbiór wartości to: \(\left(-\infty; -\frac{1}{2}\right)\cup (0; +\infty )\).
Tematy nadrzędne i sąsiednie