Przedziały

Poziom podstawowy

Definicja

Przedział otwarty \((a, b)\) - to zbiór wszystkich liczb rzeczywistych większych od \(a\) i mniejszych od \(b\).

Liczby \(a\) i \(b\) nazywamy końcami przedziału.

Na osi liczbowej przedział otwarty zaznaczamy tak:

lub tak:

Pustymi kółkami zaznaczamy, że liczby \(a\) oraz \(b\) nie należą do tego przedziału.
W przedziale otwartym nie ma liczby największej, ani liczby najmniejszej.

Zaznacz na osi liczbowej przedział \((-3,5)\).

Należy zaznaczyć zbiór tych liczb \(x\), które spełniają jednocześnie dwa warunki: \[x\gt -3\quad \text{i}\quad x\lt 5\]

Definicja

Przedział domknięty \(\langle a, b\rangle \) - to zbiór wszystkich liczb rzeczywistych, które są większe lub równe \(a\) i jednocześnie mniejsze lub równe \(b\).

Na osi liczbowej przedział domknięty zaznaczamy tak:

lub tak:

Zamalowanymi kółkami zaznaczamy, że liczby \(a\) oraz \(b\) należą do tego przedziału.
W przedziale domkniętym \(\langle a, b\rangle\) istnieje liczba najmniejsza \(a\) i liczba największa \(b\).
Przedział domknięty czasami określa się jako obustronnie domknięty.

Możemy jeszcze wyróżnić przedział lewostronnie domknięty \(\langle a, b)\):

W przedziale tym najmniejszą liczbą jest \(a\), a nie ma liczby największej.

Analogicznie wyróżniamy przedział prawostronnie domknięty \((a, b\rangle\):

W przedziale tym największą liczbą jest \(b\), a nie ma liczby najmniejszej.

Wszystkie przedziały zdefiniowane powyżej nazywamy przedziałami ograniczonymi.

Zaznacz na osi liczbowej przedział opisany nierównościami \(x\lt 0\) i \(x\geqslant -8\).

Zaznacz na osi liczbowej przedział \(x\in (1,5\rangle \).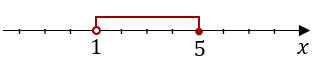

Definicja

Przedziały postaci: \((a, +\infty )\), \(\langle a, +\infty )\), \((-\infty ,a)\), \((-\infty ,a\rangle \) nazywamy przedziałami nieograniczonymi.

Ilustracje przedziałów nieograniczonych:

Przedział otwarty od \(a\) do \(+\infty \)

Przedział lewostronnie domknięty od \(a\) do \(+\infty \)

Przedział otwarty od \(-\infty \) do \(a\)

Przedział prawostronnie domknięty od \(-\infty \) do \(a\)

Przykłady przedziałów nieograniczonych otwartych: \[(2,+\infty )\qquad \left(\frac{3}{4}, +\infty \right)\qquad (-\infty, 2\sqrt{3})\]

Przykłady przedziałów nieograniczonych domkniętych: \[\langle 2,+\infty )\qquad \left\langle -\frac{1}{2}, +\infty \right)\qquad (-\infty, \sqrt{5}\rangle \]

Zbiór liczb rzeczywistych \(\mathbb{R} \) też jest przedziałem nieograniczonym i możemy go zapisać tak: \[(-\infty ,+\infty )\]