Pojęcie ciągu

Drukuj

Poziom podstawowy

Definicja

Ciągiem nieskończonym (lub krócej: ciągiem) nazywamy funkcję, której dziedziną są liczby naturalne dodatnie.
Wartości takiej funkcji nazywamy wyrazami ciągu.

Ciąg liczbowy: \[1, 4, 9, 16, 25, 36,...\] to ciąg kwadratów kolejnych liczb naturalnych.
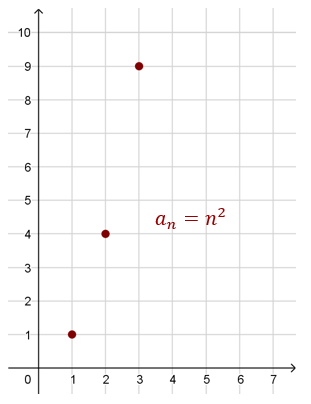
Taki ciąg to funkcja \(a: \mathbb{N} _+ \rightarrow \mathbb{R}\) dana wzorem: \[a(n)=n^2\] Kiedy mówimy o ciągu, to zazwyczaj używamy innych oznaczeń. Zamiast pisać wzór funkcji \(a(n)\), to piszemy wzór ogólny ciągu w taki sposób: \[a_n=n^2\] z którego wynika naturalne oznaczenie dla kolejnych wyrazów ciągu: \(a_1,a_2,a_3,...\).
Przykładowo:

pierwszy wyraz tego ciągu, to \(a_1=1^2=1\),
drugi wyraz tego ciągu, to \(a_2=2^2=4\),
piąty wyraz tego ciągu, to: \(a_5=5^2=25\).

Ciąg można przedstawić na wykresie:

Definicja

Wzór ogólny ciągu - to wzór na \(n\)-ty wyraz ciągu: \[a_n= \text{wzór ciągu} \]

Ciąg: \[2,4,6,8,10,12,14,...\] to ciąg kolejnych liczb parzystych dodatnich.
Wzór ogólny tego ciągu to: \(a_n=2n\).
Na przykład: drugi wyraz, to \(a_2=4\), szósty wyraz, to \(a_6=12\).

Ciąg: \[\frac{1}{2},\frac{1}{4},\frac{1}{8},\frac{1}{16},\frac{1}{32},\frac{1}{64}...\] to ciąg malejący określony wzorem: \(a_n=\frac{1}{2^n}\).
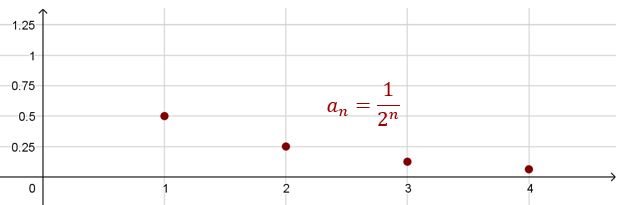
Na przykład: pierwszy wyraz, to \(a_1=\frac{1}{2}\), czwarty wyraz, to \(a_4=\frac{1}{16}\). Wykres dla tego ciągu:

Ciąg: \[3, 9, 27, 81, 243,...\] to ciąg kolejnych potęg \(3\). Wzór ogólny tego ciągu, to: \(a_n=3^n\).
Na przykład: drugi wyraz, to \(a_2=9\), piąty wyraz, to \(a_5=243\).

Możemy rozpatrywać również ciągi skończone. Jeżeli ciąg składa się z \(n\) wyrazów: \(a_!, a_2,... a_n\), to nazywamy go ciągiem \(n\)-wyrazowym.

Przykład ciągu \(3\)-wyrazowego: \(\frac{1}{2}\), \(\frac{1}{3}\), \(\frac{1}{4}\).

Przykład ciągu \(4\)-wyrazowego: \(5,9,13,17\).