Wyrażenia algebraiczne - zestaw maturalny - zadania zamknięte
Dziedziną funkcji \(f(x)=\frac{x-2}{x^2-4}\) jest zbiór
\( \mathbb{R} \backslash \{ 2 \} \)
\( (-\infty ,2) \)
\( \mathbb{R} \backslash \{-2, 2 \} \)
\( (2,0) \)
Wyrażenie \((1 - 2x)^2 - 3(x + \sqrt{2})(x - \sqrt{2})\) dla \(x = 2\) przyjmuje wartość
\( 1 \)
\( 2 \)
\( 3 \)
\( -5 \)
Rozkładając wielomian \(W(x) = x^3 - 2x^2 - 9x + 18\) na czynniki liniowe otrzymamy wielomian
\( (x+2)(x-3)(x+3) \)
\( (x+3)(x-2)(x-3) \)
\( (x-2)(x-3)(x+2) \)
\( (x+2)(x+3)(x-2) \)
Wielomian \(W(x) = x^3 + 7x^2 - 2x - 14\) po rozłożeniu na czynniki ma postać
\( W(x)=(x^2+2)(x+7) \)
\( W(x)=(x+7)(x+2)(x-2) \)
\( W(x)=(x+7)(x-\sqrt{2})(x+\sqrt{2}) \)
\( W(x)=(x-7)(x-\sqrt{2})(x+\sqrt{2}) \)
Dziedziną funkcji \(f(x)=\frac{1-x}{\sqrt{-x+6}}\) jest
\( (-\infty ,-6)\cup (6,+\infty ) \)
\( (-\infty ,6 \rangle \)
\( (-\infty ,6) \)
\( (-\infty ,-6 \rangle \)
Rozkład wielomianu \(W(x) = x^3 - 2x^2 - 16x + 32\) na czynniki liniowe to
\( (x-4)(x-4)(x-2) \)
\( (x-4)(x-2)(x+4) \)
\( (x+4)(x+2)(x+4) \)
\( (x-4)(x+4)(x+2) \)
Zbiór \(\mathbb{R} \backslash \{-3, 0, 2\}\) jest dziedziną wyrażenia
\( \frac{x^2+3x+1}{x^2+x-6} \)
\( \frac{x^2-x-2}{x^3+5x^2+6x} \)
\( \frac{3x+2}{x(x-2)(x-3)} \)
\( \frac{2x+2}{x(x-2)(x+3)} \)
Wyrażenie \(\left ( x\sqrt{2}+2x\sqrt{8} \right )^2\) jest równe
\( 18x^2 \)
\( -16x^2 \)
\( 50x^2 \)
\( 42x^2 \)
Wartość wielomianu \(W(x) = x - x^3\) dla \(x = -2\) wynosi
\( -10 \)
\( -6 \)
\( 10 \)
\( 6 \)
Które liczby ze zbioru \(\{-3, -2, -1, 0, 1, 2, 3\}\) nie należą do dziedziny poniższego wyrażenia wymiernego: \[\frac{x^2+x-5}{x^3-9x}\]
\( 0,9 \)
\( -2,-1,1,2 \)
\( -3,-1,1,3 \)
\( -3,0,3 \)
Wartość liczbowa wyrażenia algebraicznego \((a^2 - 16)(a + 2)\) dla \(a = \sqrt{2}\) wynosi
\( 56\sqrt{2} \)
\( 14(\sqrt{2}+2) \)
\( 56 \)
\( -14(\sqrt{2}+2) \)
Przedstawieniem wyrażenia \(4 - x^2 + 2xy - y^2\) w postaci iloczynu jest
\( ((x-y)-2)((x-y)+2) \)
\( ((x-y)-2)^2 \)
\( -((x-y)-2)((x-y)+2) \)
\( ((x-y)+2)^2 \)
Wyrażenie \((x-2y)(x^2+2xy+4y^2)\) jest równe
\( (x-2y)^3 \)
\( x^3+8y^3 \)
\( x^3-8y^3 \)
\( (x+2y)^3 \)
Wartość wielomianu \(W(x)=2x^4-5x^2+3x-2\) dla argumentu \(x=-2\) jest równa
\( 44 \)
\( 4 \)
\( 40 \)
\( -20 \)
Stopień wielomianu \(W(x)=(x-1)^2(2x+1)(4x^3-3)\) jest równy
\( 5 \)
\( 6 \)
\( 8 \)
\( 4 \)
Dane są wielomiany \(W(x)=4x^3+2x^2-3x-4\) oraz \(F(x)=-x^2+5x-6\).Wielomian \(G(x)=W(x)-F(x)\) jest równy:
\( -4x^3-3x^2+8x+2 \)
\( 4x^3+3x^2-8x+2 \)
\( 4x^3+3x^2-8x-2 \)
\( -4x^3-3x^2+8x-2 \)
Po skróceniu ułamek \(\frac{2x^2-4x}{x-2}\) dla \(x \ne 2\) jest równy
\( 2x^2-2 \)
\( 2x \)
\( x^2-2 \)
\( x-2 \)
Po wykonaniu działania \(\frac{x-2}{x}+\frac{x}{x+2}\) wyrażenie ma postać
\( \frac{x^2-2x}{x(x+2)} \)
\( \frac{x^2-4}{x(x+2)} \)
\( \frac{2x^2-4}{x(x+2)} \)
\( \frac{2x^2-2x}{x(x+2)} \)
Wyrażenie \(\frac{x-1}{x-2}\cdot \frac{x^2-4}{x^2-1}\) dla \(x=4\) ma wartość
\( 0 \)
\( 1\frac{1}{5} \)
\( \frac{3}{2} \)
\( 6 \)
Wyrażenie \(x^2-xy-2y+2x\) rozłożone na czynniki ma postać
\( (x-y)(x+2) \)
\( (x-y)(x-2) \)
\( (x+y)(x+2) \)
\( (x+y)(x-2) \)
Wspólny mianownik dla wyrażeń \(\frac{a}{ax-bx}\) i \(\frac{b}{ay-by}\) to
\( xy(a-b) \)
\( abxy \)
\( (a-b)(x+y) \)
\( (a-b)(x-y) \)
Wartość liczbowa wyrażenia \(x^3y^2 - y^3x^2\) dla \(x = -1\) i \(y = -2\) wynosi
\( 0 \)
\( 4 \)
\( -4 \)
\( 12 \)
Wartość wyrażenia \((a-1)(a^2+a+1)\) dla \(a=\frac{3}{4}\) jest równa
\( -\frac{37}{64} \)
\( \frac{1}{4} \)
\( -\frac{1}{4} \)
\( 1\frac{27}{64} \)
Dziedziną wyrażenia \(\frac{2-x}{(x+3)(x^2+4x+4)}\) jest zbiór:
\( \mathbb{R} \backslash \{ 2,3,-3 \} \)
\( \mathbb{R} \backslash \{ -3,2 \} \)
\( \mathbb{R} \backslash \{ -3,-2 \} \)
\( \mathbb{R} \backslash \{ -3,-2,3 \} \)
Para liczb \((x,y)\), która spełnia równanie \(x^2-2xy+y^2=25\), to
\( (-1,1) \)
\( (3,2) \)
\( (-3,-2) \)
\( (0,5) \)
Uprość wyrażenie wymierne: \(\frac{x^2+x-2}{x^2-1}\).
Niech \(x+y=12\) i \(x^2+y^2=126\). Oblicz wartość wyrażenia \(x\cdot y\).
Sprawdź czy poniższa równość jest tożsamością: \[7(x^2-2)-4(x+3)(x-3)=3x^2+22\]
Dany jest prostopadłościan, którego podstawą jest kwadrat o krawędzi długości \(x + 5\), a wysokość ma długość \(2x + 4\). Podaj wzór, w postaci wyrażenia algebraicznego, opisujący pole powierzchni tego prostopadłościanu. Przekształć to wyrażenie do najprostszej postaci.
Rozłóż na czynniki możliwie najniższego stopnia, wielomian: \(x^3+2x^2-9x-18\).
Zapisz w postaci wyrażenia algebraicznego pole zaznaczonego obszaru. 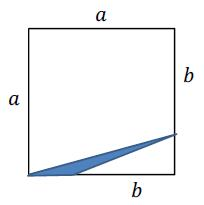

Jeden z boków prostokąta jest o \(2\) cm krótszy, a drugi o \(2\) cm dłuższy od boku pewnego kwadratu. Który z czworokątów ma większe pole i o ile większe?