Pierwiastkowanie
Poziom podstawowy
Pierwiastek oznaczamy tak: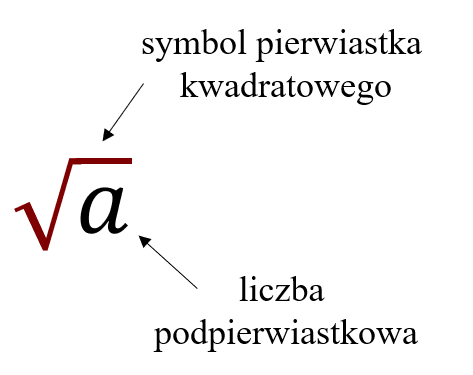 
Pierwiastek z liczby obliczamy tak, że szukamy liczby, która podniesiona do drugiej potęgi da liczbę pod pierwiastkiem.
Pierwiastek z liczby obliczamy tak, że szukamy liczby, która podniesiona do drugiej potęgi da liczbę pod pierwiastkiem. Przykład 1.
a)
\(\sqrt{4}=2\), ponieważ \(2^2=4\)b)
\(\sqrt{9}=3\), ponieważ \(3^2=9\)c)
\(\sqrt{49}=7\), ponieważ \(7^2=49\)d)
\(\sqrt{\frac{1}{16}}=\frac{1}{4}\), ponieważ \(\left(\frac{1}{4}\right )^2=\frac{1}{16}\)e)
\(\sqrt{\frac{25}{81}}=\frac{5}{9}\), ponieważ \(\left(\frac{5}{9}\right )^2=\frac{25}{81}\) Zauważmy że, wynikiem pierwiastkowania jest zawsze liczba dodatnia (lub równa zero)!
Tak samo pod pierwiastkiem może stać tylko liczba nieujemna.
Tak samo pod pierwiastkiem może stać tylko liczba nieujemna.
Jak czytamy?
Np. \(\sqrt{16}\) czytamy: pierwiastek z \(16\), lub pierwiastek kwadratowy z \(16\), lub pierwiastek drugiego stopnia z \(16\).
Przykład 2.
1)
\(\sqrt{-4}\) nie istnieje w liczbach rzeczywistych2)
\(\sqrt{-\frac{1}{9}}\) nie istnieje w liczbach rzeczywistychLekcja 1. Pierwiastki - pułapki i niebezpieczeństwa
W tym nagraniu pokazuję jakie niebezpieczeństwa mogą na nas czyhać podczas wykonywania działań na pierwiastkach.
Czas nagrania: 24 min.
Pierwiastki wyższych stopni
Możemy obliczać również pierwiastki wyższych stopni. Wtedy stosujemy taki symbol: \[ \sqrt[n]{\ \ \ \ \ \ \ } \] gdzie \(n\) – to stopień pierwiastka.Aby pierwiastek był określony w liczbach rzeczywistych, gdy \(n\) jest parzyste, liczba pod pierwiastkiem musi być nieujemna. Pierwiastki nieparzystych stopni możemy obliczać również z liczb ujemnych.
Chcąc obliczyć pierwiastek \(n\)-tego stopnia, szukamy liczby, która podniesiona do \(n\)-tej potęgi da wartość pod pierwiastkiem.
Przykład 3.
a)
\(\sqrt[3]{8}=2\), ponieważ \(2^3=8\)b)
\(\sqrt[3]{-27}=-3\), ponieważ \((-3)^3=-27\)c)
\(\sqrt[5]{-1}=-1\), ponieważ \((-1)^5=-1\)d)
\(\sqrt[4]{\frac{1}{16}}=\frac{1}{2}\), ponieważ \(\left(\frac{1}{2}\right)^4=\frac{1}{16}\)e)
\(\sqrt[4]{\frac{625}{81}}=\frac{5}{3}\), ponieważ \(\left(\frac{5}{3}\right)^4=\frac{625}{81}\)Zapis pierwiastka za pomocą potęgi
\[ \sqrt[n]{a}=a^{\frac{1}{n}} \]Przykład 4.
a)
\(\sqrt[3]{8}=8^{\frac{1}{3}}\)b)
\(\sqrt[5]{x}=x^{\frac{1}{5}}\)c)
\(\sqrt[7]{a\cdot b^2}=(a\cdot b^2)^{\frac{1}{7}}\)d)
\(\sqrt{13x}=(13x)^{\frac{1}{2}}\) Dzięki zapisowi za pomocą potęg możemy łatwiej wykonywać działania na pierwiastkach, korzystając z reguł działań na potęgach.
Przykład 5.
- \(\sqrt[3]{x}\cdot \sqrt[5]{x}=x^{\frac{1}{3}}\cdot x^{\frac{1}{5}}=x^{\frac{1}{3}+\frac{1}{5}}=x^{\frac{8}{15}}\)
- \(\frac{\sqrt[4]{x^3}}{\sqrt[6]{x}}=x^{\frac{3}{4}-\frac{1}{6}}=x^{\frac{9}{12}-\frac{2}{12}}=x^{\frac{7}{12}}\)
- \(\sqrt[4]{x}\cdot \sqrt[4]{x^3}=x^{\frac{1}{4}}\cdot x^{\frac{3}{4}}=x^{\frac{1}{4}+\frac{3}{4}}=x^1=x\) określone dla \(x\ge 0\)
Własności działań na pierwiastkach
Dla liczb nieujemnych zachodzą następujące własności:
- \(\sqrt[n]{a}\cdot\sqrt[n]{b}=\sqrt[n]{ab}\)
- \(\frac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\frac{a}{b}}\) (dla \(b\neq 0\))
- \(\sqrt[n]{a^n}=|a|\) dla \(n\) parzystych oraz \(\sqrt[n]{a^n}=a\) dla \(n\) nieparzystych.
Upraszczanie pierwiastków
Aby uprościć pierwiastek, rozkładamy liczbę pod pierwiastkiem na czynniki i wyciągamy te, które są doskonałymi potęgami odpowiadającymi stopniowi pierwiastka. Przykłady:
Przykład 6.
a)
\(\sqrt{72}=\sqrt{36\cdot2}=6\sqrt{2}\)b)
\(\sqrt[3]{54}=\sqrt[3]{27\cdot2}=3\sqrt[3]{2}\)Dodawanie i odejmowanie wyrażeń z pierwiastkami
Możemy dodawać lub odejmować tylko wyrażenia zawierające te same pierwiastki (tzn. te, które mają taki sam indeks i radikand). Przykłady:
Przykład 7.
a)
\(2\sqrt{3}+5\sqrt{3}=7\sqrt{3}\)b)
\(4\sqrt{2}-\sqrt{2}=3\sqrt{2}\)c)
\(3\sqrt{5}+2\sqrt{3}\) nie można uprościć, ponieważ liczby pod pierwiastkami są różne.Mnożenie i dzielenie wyrażeń z pierwiastkami
Mnożenie i dzielenie wykonujemy, korzystając z własności pierwiastków:
Przykład 8.
\[ \sqrt{a}\cdot\sqrt{b}=\sqrt{ab},\quad \frac{\sqrt{a}}{\sqrt{b}}=\sqrt{\frac{a}{b}} \]
Usuwanie niewymierności z mianownika
Jeżeli w mianowniku ułamka znajduje się pierwiastek, często dążymy do usunięcia tego pierwiastka.
Przykład 9.
a)
\(\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}\)b)
\(\frac{3}{2\sqrt{5}}=\frac{3\sqrt{5}}{10}\)Ułamki z pierwiastkami w liczniku i mianowniku
Często upraszczamy wyrażenia, gdzie zarówno licznik, jak i mianownik zawierają pierwiastki. Wykorzystujemy do tego własności działań na pierwiastkach i racjonalizację mianownika. Przykłady:
Przykład 10.
a)
\(\frac{\sqrt{18}}{\sqrt{8}}=\frac{\sqrt{9\cdot2}}{\sqrt{4\cdot2}}=\frac{3\sqrt{2}}{2\sqrt{2}}=\frac{3}{2}\) b)
\(\frac{2\sqrt{3}+\sqrt{12}}{\sqrt{3}}=\frac{2\sqrt{3}+2\sqrt{3}}{\sqrt{3}}=\frac{4\sqrt{3}}{\sqrt{3}}=4\) Równania z pierwiastkami
W równaniach zawierających pierwiastki najczęściej izolujemy pierwiastek po jednej stronie równania, a następnie podnosimy obie strony do potęgi odpowiadającej stopniowi pierwiastka. Pamiętamy jednak, że takie działanie może wykonać tylko jak obie strony równania są tego samego znaku! W tym celu wyznaczamy dziedzinę.
Przykład 11.
a)
Rozwiąż równanie: \(\sqrt{x+5}=3\). - Dziedzina: \(x+5\ge 0\), więc \(x\ge -5\).
- Podnosimy obie strony do kwadratu: \(x+5=9\).
- Otrzymujemy: \(x=4\) - rozwiązanie należy do dziedziny.
- Sprawdzamy: \(\sqrt{4+5}=\sqrt{9}=3\).
b)
Rozwiąż równanie: \(\sqrt[3]{2x-1}=3\). - Stopień pierwiastka jest nieparzysty, więc dziedziną jest całe \(\mathbb{R} \).
- Podnosimy obie strony do potęgi trzeciej: \(2x-1=27\).
- Otrzymujemy: \(2x=28\), czyli \(x=14\).
- Sprawdzamy: \(\sqrt[3]{2\cdot14-1}=\sqrt[3]{27}=3\).
Zadanie 1.
Uzupełnij poniższe zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Wyrażenie \(\sqrt{81}-\sqrt{49}\) jest równe A
B
. A.\( 2 \)
B.\( \sqrt{32} \)
C
D
. C.\( 13 \)
D.\( 17 \)
Zadanie 2.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba \(3\sqrt{45}-\sqrt{20}\) jest równa A.\( (7\cdot 5)^{\frac{1}{2}} \)
B.\( 5^{\frac{1}{2}} \)
C.\( 7 \)
D.\( 7\cdot 5^{\frac{1}{2}} \)
Zadanie 3.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Dla każdej dodatniej liczby rzeczywistej \(x\) iloczyn \(\sqrt{x}\cdot \sqrt[3]{x}\cdot \sqrt[6]{x}\) jest równy A.\( x \)
B.\( \sqrt[10]{x} \)
C.\( \sqrt[18]{x} \)
D.\( x^2 \)
Zadanie 4.
Liczba \(\sqrt[3]{\frac{7}{3}}\cdot \sqrt[3]{\frac{81}{56}}\) jest równa
A.\( \frac{3}{2} \)
B.\( \frac{9}{4} \)
C.\( \frac{\sqrt{3}}{2} \)
D.\( \frac{3}{2\sqrt[3]{21}} \)
Zadanie 5.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba \(\sqrt[3]{-\frac{27}{16}}\cdot \sqrt[3]{2}\) jest równa A.\( \left(-\frac{3}{2}\right) \)
B.\( \frac{3}{2} \)
C.\( \frac{2}{3} \)
D.\( \left(-\frac{2}{3}\right) \)
Zadanie 6.
Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych.
Liczba \(\frac{\sqrt[3]{250}+\sqrt[3]{54}}{\sqrt[3]{250}-\sqrt[3]{54}}\) jest równa A.\(\sqrt[3]{\frac{76}{49}}\)
B.\( (-1) \)
C.\( 4 \)
D.\( 4 \sqrt[3]{2} \)
Zadanie 7.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba \(\left(\sqrt[5]{5} \cdot \frac{1}{5}\right)^{-5}\) jest równa A.\(5^{4}\)
B.\(5^{-4}\)
C.\(5^{0,25}\)
D.\(5^{-0,25}\)
Zadanie 8.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba \((2 \sqrt{10}+\sqrt{2})^{2}\) jest równa A.22
B.42
C.\(42+4 \sqrt{5}\)
D.\(42+8 \sqrt{5}\)
Zadanie 9.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Wartość wyrażenia \((2-\sqrt{3})^2-(\sqrt{3}-2)^2\) jest równa A.\( (-2\sqrt{3}) \)
B.\( 0 \)
C.\( 6 \)
D.\( 8\sqrt{3} \)
Zadanie 10.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba \((1+\sqrt{5})^2-(1-\sqrt{5})^2\) jest równa A.\( 0 \)
B.\( (-10) \)
C.\( 4\sqrt{5} \)
D.\( 2+2\sqrt{5} \)
Tematy nadrzędne i sąsiednie