Obliczanie wartości funkcji trygonometrycznych dla kątów od 0° do 360°
Poziom rozszerzony
Dowolny kąt można utożsamić z kątem z przedziału \(\left \langle 0^\circ , 360^\circ \right \rangle\).Jeżeli kąt \(\alpha \in \left \langle 0^\circ , 360^\circ \right \rangle\), to jego ramiona pokrywają się z ramionami kąta o mierze \(\alpha + k\cdot 360^\circ \), gdzie \(k\in \mathbb{Z} \).
Twierdzenie
Dla \(k\in \mathbb{Z} \) zachodzi: \[ \sin (\alpha +k\cdot 360^\circ )=\sin \alpha \\[6pt] \cos (\alpha +k\cdot 360^\circ )=\cos \alpha \\[6pt] \operatorname{tg} (\alpha +k\cdot 360^\circ )=\operatorname{tg} \alpha\\[6pt] \operatorname{ctg} (\alpha +k\cdot 360^\circ )=\operatorname{ctg} \alpha \\[6pt] \] Dla tangensa i cotangensa mamy nawet: \[\begin{split} &\operatorname{tg} (\alpha +k\cdot 180^\circ )=\operatorname{tg} \alpha \\[6pt]&\operatorname{ctg} (\alpha +k\cdot 180^\circ )=\operatorname{ctg} \alpha \\[6pt] \end{split}\] Wzory na są tangens są określone dla \(\alpha \ne \frac{\pi}{2}+k\pi\), a na cotangens dla dla \(\alpha \ne k\pi\). Każdą funkcję trygonometryczną kąta większego od \(360^\circ \) możemy zamienić na równoważną funkcję trygonometryczną kąta z przedziału \(\left \langle 0^\circ , 360^\circ \right \rangle\). Przykładowo:
- \(\sin 400^\circ = \sin (40^\circ +360^\circ )=\sin 40^\circ \)
- \(\cos 442^\circ = \cos (82^\circ +360^\circ )=\cos 82^\circ \)
- \(\operatorname{tg} 1180^\circ = \operatorname{tg} (100^\circ +3\cdot 360^\circ )=\operatorname{tg} 100^\circ \)
- \(\operatorname{ctg} (-510^\circ) = \operatorname{ctg} (210^\circ -2\cdot 360^\circ )=\operatorname{ctg} 210^\circ \)
Zatem obliczanie wartość trygonometrycznych dowolnych kątów sprowadza się do obliczania wartości trygonometrycznych ich kątów tożsamych w przedziale \(\left \langle 0^\circ , 360^\circ \right \rangle\).
Wartości funkcji trygonometrycznych dla kątów z przedziału \(\left \langle 0^\circ , 360^\circ \right \rangle\), można sprowadzić jedynie do przedziału \(\left \langle 0^\circ , 90^\circ \right \rangle\) za pomocą wzorów redukcyjnych. Wzorów tych jest bardzo dużo i możesz je znaleźć w zestawieniu wzorów trygonometrycznych. Poniżej zamieszczam najważniejsze z nich.
Wybrane wzory redukcyjne
| \[\begin{split}&\sin{\left ( 90^\circ +\alpha \right )}=\cos{\alpha }\\[12pt] &\cos{\left ( 90^\circ +\alpha \right )}=-\sin{\alpha }\\[12pt] &\text{tg}{\left ( 90^\circ +\alpha \right )}=-\text{ctg}{\alpha }\\[12pt] &\text{ctg}{\left ( 90^\circ +\alpha \right )}=-\text{tg}{\alpha } \end{split}\] | \[\begin{split} &\sin{\left ( 90^\circ -\alpha \right )}=\cos{\alpha }\\[12pt] &\cos{\left ( 90^\circ -\alpha \right )}=\sin{\alpha }\\[12pt] &\text{tg}{\left ( 90^\circ -\alpha \right )}=\text{ctg}{\alpha }\\[12pt] &\text{ctg}{\left ( 90^\circ -\alpha \right )}=\text{tg}{\alpha } \end{split}\] | |
| \[\begin{split} &\sin{\left ( 180^\circ +\alpha \right )}=-\sin{\alpha }\\[12pt] &\cos{\left ( 180^\circ +\alpha \right )}=-\cos{\alpha }\\[12pt] &\text{tg}{\left ( 180^\circ +\alpha \right )}=\text{tg}{\alpha }\\[12pt] &\text{ctg}{\left ( 180^\circ +\alpha \right )}=\text{ctg}{\alpha } \end{split}\] | \[\begin{split} &\sin{\left ( 180^\circ -\alpha \right )}=\sin{\alpha }\\[12pt] &\cos{\left ( 180^\circ -\alpha \right )}=-\cos{\alpha }\\[12pt] &\text{tg}{\left ( 180^\circ -\alpha \right )}=-\text{tg}{\alpha }\\[12pt] &\text{ctg}{\left ( 180^\circ -\alpha \right )}=-\text{ctg}{\alpha } \end{split}\] |
\[\begin{split}&\sin{\left ( 90^\circ +\alpha \right )}=\cos{\alpha }\\[12pt] &\cos{\left ( 90^\circ +\alpha \right )}=-\sin{\alpha }\\[12pt] &\text{tg}{\left ( 90^\circ +\alpha \right )}=-\text{ctg}{\alpha }\\[12pt] &\text{ctg}{\left ( 90^\circ +\alpha \right )}=-\text{tg}{\alpha }\\[12pt] &\sin{\left ( 90^\circ -\alpha \right )}=\cos{\alpha }\\[12pt] &\cos{\left ( 90^\circ -\alpha \right )}=\sin{\alpha }\\[12pt] &\text{tg}{\left ( 90^\circ -\alpha \right )}=\text{ctg}{\alpha }\\[12pt] &\text{ctg}{\left ( 90^\circ -\alpha \right )}=\text{tg}{\alpha }\\[22pt] &\sin{\left ( 180^\circ +\alpha \right )}=-\sin{\alpha }\\[12pt] &\cos{\left ( 180^\circ +\alpha \right )}=-\cos{\alpha }\\[12pt] &\text{tg}{\left ( 180^\circ +\alpha \right )}=\text{tg}{\alpha }\\[12pt] &\text{ctg}{\left ( 180^\circ +\alpha \right )}=\text{ctg}{\alpha }\\[12pt] &\sin{\left ( 180^\circ -\alpha \right )}=\sin{\alpha }\\[12pt] &\cos{\left ( 180^\circ -\alpha \right )}=-\cos{\alpha }\\[12pt] &\text{tg}{\left ( 180^\circ -\alpha \right )}=-\text{tg}{\alpha }\\[12pt] &\text{ctg}{\left ( 180^\circ -\alpha \right )}=-\text{ctg}{\alpha } \end{split}\]
Teraz na kilku przykładach pokażę jak można wyprowadzać wzory redukcyjne wprost z definicji.
Oblicz \(\sin 150^\circ \text{, }\cos 150^\circ \text{ i} \operatorname{tg} 150^\circ \).
Zaczynamy od zaznaczenia w układzie współrzędnych kąta \(150^\circ \). Narysujmy również okrąg jednostkowy (o promieniu 1).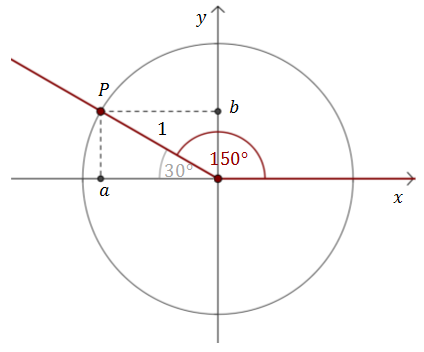 
Na przecięciu ramienia kąta i okręgu możemy zaznaczyć punkt \(P=(a,b)\).
Z definicji funkcji trygonometrycznych wiemy, że: \[\begin{split} &\sin 150^\circ =\frac{b}{1}=b\\[6pt]&\cos 150^\circ =\frac{a}{1}=a\\[6pt]&\operatorname{tg} 150^\circ =\frac{b}{a}\\[6pt] \end{split}\] Nie znamy na razie współrzędnych \(a\text{ i }b\), ale możemy zauważyć, że jak odbijemy punkt \(P\) względem osi \(Oy\), to otrzymamy rysunek: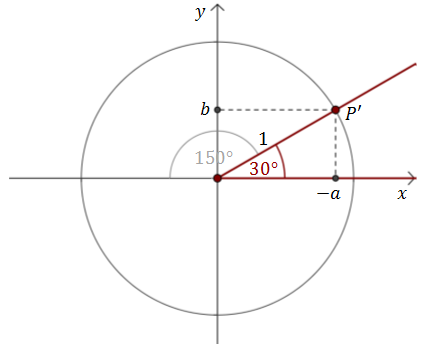
Dla kąta \(30^\circ \) liczymy, że: \[\begin{split} &\sin 30^\circ =\frac{b}{1}=b\\[6pt]&\cos 30^\circ =\frac{-a}{1}=-a\\[6pt]&\operatorname{tg} 30^\circ =\frac{b}{-a}\\[6pt] \end{split}\] Zatem: \[\begin{split} &\sin 150^\circ =\sin 30^\circ =\frac{1}{2}\\[6pt]&\cos 150^\circ =-\cos 30^\circ =-\frac{\sqrt{3}}{2}\\[6pt]&\operatorname{tg} 150^\circ =-\operatorname{tg} 30^\circ =-\frac{\sqrt{3}}{3}\\[6pt] \end{split}\]
Na przecięciu ramienia kąta i okręgu możemy zaznaczyć punkt \(P=(a,b)\).Z definicji funkcji trygonometrycznych wiemy, że: \[\begin{split} &\sin 150^\circ =\frac{b}{1}=b\\[6pt]&\cos 150^\circ =\frac{a}{1}=a\\[6pt]&\operatorname{tg} 150^\circ =\frac{b}{a}\\[6pt] \end{split}\] Nie znamy na razie współrzędnych \(a\text{ i }b\), ale możemy zauważyć, że jak odbijemy punkt \(P\) względem osi \(Oy\), to otrzymamy rysunek:
Dla kąta \(30^\circ \) liczymy, że: \[\begin{split} &\sin 30^\circ =\frac{b}{1}=b\\[6pt]&\cos 30^\circ =\frac{-a}{1}=-a\\[6pt]&\operatorname{tg} 30^\circ =\frac{b}{-a}\\[6pt] \end{split}\] Zatem: \[\begin{split} &\sin 150^\circ =\sin 30^\circ =\frac{1}{2}\\[6pt]&\cos 150^\circ =-\cos 30^\circ =-\frac{\sqrt{3}}{2}\\[6pt]&\operatorname{tg} 150^\circ =-\operatorname{tg} 30^\circ =-\frac{\sqrt{3}}{3}\\[6pt] \end{split}\] Algorytm
Żeby obliczyć z definicji wartości funkcji trygonometrycznych dla kąta rozwartego \(\alpha \) , należy:- Narysować w układzie współrzędnych okrąg jednostkowy i zaznaczyć w nim kąt środkowy \(\alpha \) .
- Zaznaczyć punkt \(P\), czyli punkt przecięcia okręgu i ramienia kąta.
- Znaleźć w pierwszej ćwiartce punkt \(P'\) - symetryczny obraz punktu \(P\) (symetria może być względem dowolnej osi lub początku układu współrzędnych).
- Obliczyć wartości funkcji trygonometrycznych dla kąta \(\beta \) wyznaczonego przez punkt \(P'\).
- Wyrazić funkcje trygonometryczne kąta \(\alpha \) za pomocą funkcji trygonometrycznych kąta \(\beta \).
Oblicz \(\sin 230^\circ \text{, }\cos 230^\circ \text{ i} \operatorname{tg} 230^\circ \).
Rysujmy w układzie współrzędnych okrąg jednostkowy i zaznaczamy w nim kąt środkowy o mierze \(230^\circ \).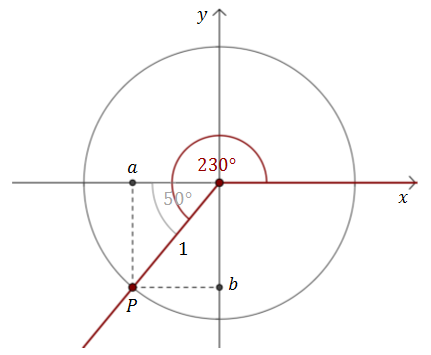 
Na przecięciu ramienia kąta i okręgu zaznaczamy punkt \(P=(a,b)\).
Z definicji funkcji trygonometrycznych wiemy, że: \[\begin{split} &\sin 230^\circ =\frac{b}{1}=b\\[6pt]&\cos 230^\circ =\frac{a}{1}=a\\[6pt]&\operatorname{tg} 230^\circ =\frac{b}{a}\\[6pt] \end{split}\] Odbijamy punkt \(P\) względem początku układu współrzędnych i otrzymujemy punkt \(P'=(-a,-b)\).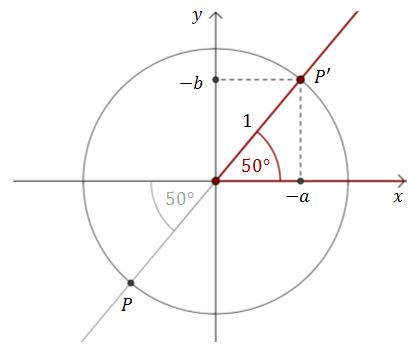
Wyznaczamy wartości funkcji trygonometrycznych dla kąta \(50^\circ \): \[\begin{split} &\sin 50^\circ =\frac{-b}{1}=-b\\[6pt]&\cos 50^\circ =\frac{-a}{1}=-a\\[6pt]&\operatorname{tg} 50^\circ =\frac{-b}{-a}=\frac{b}{a}\\[6pt] \end{split}\] Zatem: \[\begin{split} &\sin 230^\circ =-\sin 50^\circ\\[6pt]&\cos 230^\circ =-\cos 50^\circ\\[6pt]&\operatorname{tg} 230^\circ =\operatorname{tg} 50^\circ\\[6pt] \end{split}\] Wartości funkcji trygonometrycznych dla kąta \(50^\circ \) możemy odczytać z tablic trygonometrycznych.
Na przecięciu ramienia kąta i okręgu zaznaczamy punkt \(P=(a,b)\).Z definicji funkcji trygonometrycznych wiemy, że: \[\begin{split} &\sin 230^\circ =\frac{b}{1}=b\\[6pt]&\cos 230^\circ =\frac{a}{1}=a\\[6pt]&\operatorname{tg} 230^\circ =\frac{b}{a}\\[6pt] \end{split}\] Odbijamy punkt \(P\) względem początku układu współrzędnych i otrzymujemy punkt \(P'=(-a,-b)\).
Wyznaczamy wartości funkcji trygonometrycznych dla kąta \(50^\circ \): \[\begin{split} &\sin 50^\circ =\frac{-b}{1}=-b\\[6pt]&\cos 50^\circ =\frac{-a}{1}=-a\\[6pt]&\operatorname{tg} 50^\circ =\frac{-b}{-a}=\frac{b}{a}\\[6pt] \end{split}\] Zatem: \[\begin{split} &\sin 230^\circ =-\sin 50^\circ\\[6pt]&\cos 230^\circ =-\cos 50^\circ\\[6pt]&\operatorname{tg} 230^\circ =\operatorname{tg} 50^\circ\\[6pt] \end{split}\] Wartości funkcji trygonometrycznych dla kąta \(50^\circ \) możemy odczytać z tablic trygonometrycznych. Oblicz \(\sin 315^\circ \text{, }\cos 315^\circ \text{ i} \operatorname{tg} 315^\circ \).
Rysujmy w układzie współrzędnych okrąg jednostkowy i zaznaczamy w nim kąt środkowy o mierze \(315^\circ \).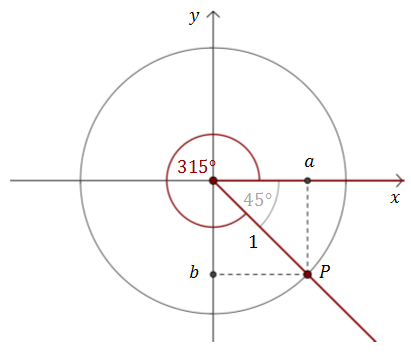 
Na przecięciu ramienia kąta i okręgu zaznaczamy punkt \(P=(a,b)\).
Z definicji funkcji trygonometrycznych wiemy, że: \[\begin{split} &\sin 315^\circ =\frac{b}{1}=b\\[6pt]&\cos 315^\circ =\frac{a}{1}=a\\[6pt]&\operatorname{tg} 315^\circ =\frac{b}{a}\\[6pt] \end{split}\] Odbijamy punkt \(P\) względem osi \(Ox\) i otrzymujemy punkt \(P'=(a,-b)\).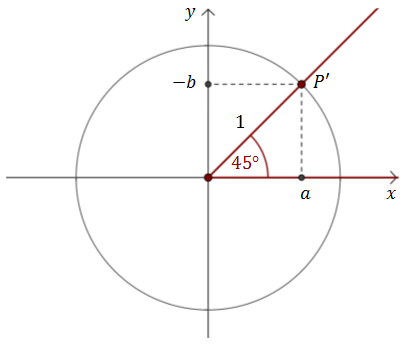
Wyznaczamy wartości funkcji trygonometrycznych dla kąta \(45^\circ \): \[\begin{split} &\sin 45^\circ =\frac{-b}{1}=-b\\[6pt]&\cos 45^\circ =\frac{a}{1}=a\\[6pt]&\operatorname{tg} 45^\circ =\frac{-b}{a}=-\frac{b}{a}\\[6pt] \end{split}\] Zatem: \[\begin{split} &\sin 315^\circ =-\sin 45^\circ=-\frac{\sqrt{2}}{2}\\[6pt]&\cos 315^\circ =\cos 45^\circ=\frac{\sqrt{2}}{2}\\[6pt]&\operatorname{tg} 315^\circ =-\operatorname{tg} 45^\circ=-1\\[6pt] \end{split}\]
Na przecięciu ramienia kąta i okręgu zaznaczamy punkt \(P=(a,b)\).Z definicji funkcji trygonometrycznych wiemy, że: \[\begin{split} &\sin 315^\circ =\frac{b}{1}=b\\[6pt]&\cos 315^\circ =\frac{a}{1}=a\\[6pt]&\operatorname{tg} 315^\circ =\frac{b}{a}\\[6pt] \end{split}\] Odbijamy punkt \(P\) względem osi \(Ox\) i otrzymujemy punkt \(P'=(a,-b)\).
Wyznaczamy wartości funkcji trygonometrycznych dla kąta \(45^\circ \): \[\begin{split} &\sin 45^\circ =\frac{-b}{1}=-b\\[6pt]&\cos 45^\circ =\frac{a}{1}=a\\[6pt]&\operatorname{tg} 45^\circ =\frac{-b}{a}=-\frac{b}{a}\\[6pt] \end{split}\] Zatem: \[\begin{split} &\sin 315^\circ =-\sin 45^\circ=-\frac{\sqrt{2}}{2}\\[6pt]&\cos 315^\circ =\cos 45^\circ=\frac{\sqrt{2}}{2}\\[6pt]&\operatorname{tg} 315^\circ =-\operatorname{tg} 45^\circ=-1\\[6pt] \end{split}\] Tematy nadrzędne i sąsiednie