Tożsamości trygonometryczne

Drukuj

Poziom rozszerzony

Tożsamość trygonometryczna – to równość, w której występują funkcje trygonometryczne i która jest prawdziwa dla wszystkich zmiennych, dla których wyrażenia występujące w tej równości mają sens.

Podstawowe tożsamości trygonometryczne

\(\sin ^{2} x+\cos ^{2} x=1\) dla dowolnego \(x \in \mathbb{R} \quad\) (jedynka trygonometryczna)
\(\operatorname{tg} x=\frac{\sin x}{\cos x}\) dla \(x \in \mathbb{R} \backslash\left\{\frac{\pi}{2}+k \pi: k \in \mathbb{Z}\right\}\)
\(\operatorname{ctg} x=\frac{\cos x}{\sin x}\) dla \(x \in \mathbb{R} \backslash\{k \pi: k \in \mathbb{Z}\}\)
\(\operatorname{ctg} x=\frac{1}{\operatorname{tg} x}\) oraz \(\operatorname{tg} x=\frac{1}{\operatorname{ctg} x}\) dla \(x \in \mathbb{R} \backslash\left\{\frac{k \pi}{2}: k \in \mathbb{Z} \right\}\)

Każdą tożsamość trygonometryczną można udowodnić korzystając bezpośrednio z definicji funkcji trygonometrycznych

Wykaż, że zachodzi jedynka trygonometryczna \(\sin ^{2} x+\cos ^{2} x=1\) dla dowolnego \(x \in \mathbf{R} \quad\)

Niech punkt \(P\left(x_0,y_0\right)\), będzie punktem na ramieniu kąta \(x\).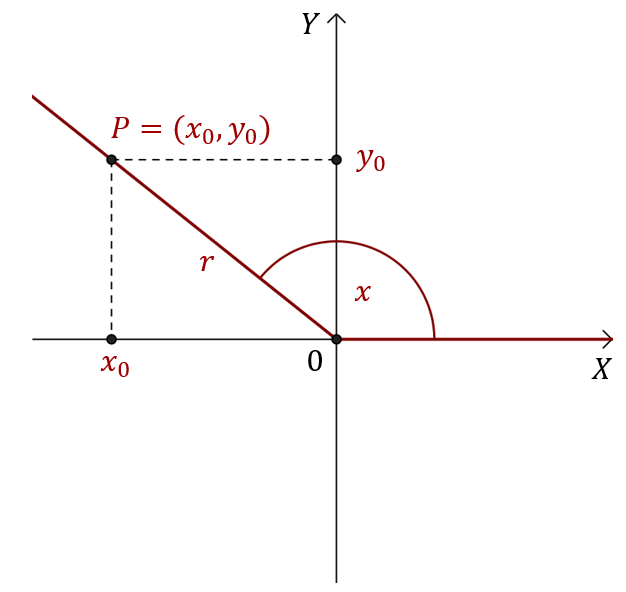

Wówczas z definicji mamy: \[\sin{x}=\frac{y_0}{r}\qquad \qquad \cos{x}=\frac{x_0}{r}\] gdzie \(r=\sqrt{x_0^2+y_0^2}\).
Zatem:

\[ \sin ^{2} x+\cos ^{2} x=\left(\frac{y_{0}}{r}\right)^{2}+\left(\frac{x_{0}}{r}\right)^{2}=\frac{y_{0}^{2}+x_{0}^{2}}{r^{2}}=\frac{x_{0}^{2}+y_{0}^{2}}{\left(\sqrt{x_{0}^{2}+y_{0}^{2}}\right)^{2}}=1\ _{c.n.d.} \]

\[ \sin ^{2} x+\cos ^{2} x=\left(\frac{y_{0}}{r}\right)^{2}+\left(\frac{x_{0}}{r}\right)^{2}=\\[6pt] =\frac{y_{0}^{2}+x_{0}^{2}}{r^{2}}=\frac{x_{0}^{2}+y_{0}^{2}}{\left(\sqrt{x_{0}^{2}+y_{0}^{2}}\right)^{2}}=1\ _{c.n.d.} \]

Podobnie można pokazać, że zachodzi \(\operatorname{tg} x=\frac{\sin x}{\cos x}\) dla \(x \in \mathbb{R} \backslash\left\{\frac{\pi}{2}+k \pi: k \in \mathbb{Z}\right\}\).
Wystarczy skorzystać z definicji \(\operatorname{tg}=\frac{y_0}{x_0}\) oraz definicji sinusa i cosinusa: \[\frac{\sin x}{\cos x}=\frac{\frac{y_0}{r}}{\frac{x_0}{r}}=\frac{y_0}{x_0}=\operatorname{tg} x\] Dziedziną powyższego wyrażenia są wszystkie miary kąta \(x\), dla których \(x_0\ne 0\). Na powyższym wykresie widać, że \(x_0=0\Leftrightarrow x=\frac{\pi}{2}+k \pi\) dla \(k \in \mathbb{Z}\).

Przy dowodzeniu tożsamości trygonometrycznych nie trzeba korzystać z definicji funkcji trygonometrycznych. Możemy korzystać ze znanych wzorów, takich jak np.: jedynka trygonometryczna lub wzór na tangens.

Udowodnij tożsamość trygonometryczną.

\((1-\sin ^{2} x) \operatorname{tg} x=\sin x \cos x\)
\((1-\operatorname{tg} x)(1+\operatorname{ctg} x)=\operatorname{ctg} x-\operatorname{tg} x\)

Korzystamy z jedynki trygonometrycznej i wzoru na tangens:
\[(1-\sin ^{2} x) \operatorname{tg} x =(\sin ^{2} x+\cos ^{2} x-\sin ^{2} x)\cdot \frac{\sin x}{\cos x} =\cos ^{2} x\cdot \frac{\sin x}{\cos x} =\cos x\cdot \sin x\ _{c.n.d.} \]

\[\begin{split} &(1-\sin ^{2} x) \operatorname{tg} x=\\[6pt] &=(\sin ^{2} x+\cos ^{2} x-\sin ^{2} x)\cdot \frac{\sin x}{\cos x}=\\[6pt] &=\cos ^{2} x\cdot \frac{\sin x}{\cos x}=\\[6pt] &=\cos x\cdot \sin x\ _{c.n.d.}\end{split}\]
Ta tożsamość zachodzi dla \(x \in \mathbf{R} \backslash\left\{\frac{\pi}{2}+k \pi: k \in \mathbf{Z}\right\}\)
Wymnażamy nawiasy, a następnie korzystamy z własności: \(\operatorname{tg}x\cdot \operatorname{ctg}x=\operatorname{tg}x\cdot \frac{1}{\operatorname{tg}x}=1\)
\[ (1-\operatorname{tg} x)(1+\operatorname{ctg} x) = 1+\operatorname{ctg}x-\operatorname{tg}x-\operatorname{tg}x\cdot \operatorname{ctg}x = 1+\operatorname{ctg}x-\operatorname{tg}x- 1 = \operatorname{ctg}x-\operatorname{tg}x\ _{c.n.d.} \]

\[ \begin{split} &(1-\operatorname{tg} x)(1+\operatorname{ctg} x)=\\[6pt] &= 1+\operatorname{ctg}x-\operatorname{tg}x-\operatorname{tg}x\cdot \operatorname{ctg}x=\\[6pt] &= 1+\operatorname{ctg}x-\operatorname{tg}x- 1=\\[6pt] &= \operatorname{ctg}x-\operatorname{tg}x\ _{c.n.d.}\end{split}\]
Ta tożsamość jest określona dla \(x \in \mathbf{R} \backslash\left\{\frac{k \pi}{2}: k \in \mathbf{Z}\right\}\)

Udowodnij, że \(\cos ^{4} x-\sin ^{4} x=\cos ^{2} x- \sin ^{2} x\).

Lewą stronę przekształcamy wzorem skróconego mnożenia, a następnie stosujemy jedynkę trygonometryczną. \[ \begin{split} &\cos ^{4} x-\sin ^{4} x=\\[6pt] &=\left(\cos ^{2} x-\sin ^{2} x\right)\left(\cos ^{2} x+\sin ^{2} x\right)=\\[6pt] &=\left(\cos ^{2} x-\sin ^{2} x\right)\cdot 1=\\[6pt] &= \cos ^{2} x-\sin ^{2} \end{split} \]

Czasami, aby udowodnić tożsamość trygonometryczną, warto przekształcić zarówno prawą, jak i jej lewą stronę.

Udowodnij tożsamość: \(\frac{(\sin x+\cos x)^2}{\sin x \cos x}-2=\operatorname{tg} x+\frac{\cos x}{\sin x}\)

Zakładamy, że wyrażenie jest określone, czyli, że: \(\sin x \ne 0\) oraz \(\cos x \ne 0\). Tak jest dla \(x \in \mathbf{R} \backslash\left\{\frac{k \pi}{2}: k \in \mathbf{Z}\right\}\).

Przekształcamy lewą stronę: \[L=\frac{(\sin x+\cos x)^2}{\sin x \cos x}-2\] Podnosimy licznik do kwadratu, sprowadzamy ułamki do wspólnego mianownika oraz stosujemy wzór na jedynkę trygonometryczną:

\[ \begin{split} &L=\frac{(\sin x+\cos x)^2}{\sin x \cos x}-2=\\[6pt] &=\frac{\sin ^2 x+2 \sin x \cos x+\cos ^2 x}{\sin x \cos x}-\frac{2\sin x \cos x}{\sin x \cos x}=\\[6pt] &= \frac{\sin ^2 x+\cos ^2 x}{\sin x \cos x}=\\[6pt] &= \frac{1}{\sin x \cos x} \end{split}\]

\[ \begin{split} &L=\frac{(\sin x+\cos x)^2}{\sin x \cos x}-2=\\[6pt] &=\frac{\sin ^2 x+2 \sin x \cos x+\cos ^2 x}{\sin x \cos x}\\[6pt] &-\frac{2\sin x \cos x}{\sin x \cos x}=\\[6pt] &= \frac{\sin ^2 x+\cos ^2 x}{\sin x \cos x}=\\[6pt] &= \frac{1}{\sin x \cos x} \end{split}\]

Przekształcamy prawą stronę: \[P=\operatorname{tg} x+\frac{\cos x}{\sin x}\] Stosujemy wzór na tangens, sprowadzamy ułamki do wspólnego mianownika oraz stosujemy wzór na jedynkę trygonometryczną: \[ \begin{split} &P=\operatorname{tg} x+\frac{\cos x}{\sin x}=\\[6pt] &=\frac{\sin x}{\cos x}+\frac{\cos x}{\sin x}=\\[6pt] &=\frac{\sin^2 x}{\cos x\cdot \sin x}+\frac{\cos^2 x}{\sin x\cdot \cos x}=\\[6pt] &=\frac{\sin^2 x+\cos^2 x}{\sin x\cdot \cos x}=\\[6pt] &= \frac{1}{\sin x \cos x} \end{split}\] Zatem zachodzi równość \(L = P\)

Udowodnij tożsamość: \(\frac{1+2 \sin x \cos x}{\cos ^{2} x}=(1+\operatorname{tg} x)^{2}\)

Zakładamy, że wyrażenie jest określone, czyli, że: \(\cos x \ne 0\). Tak jest dla \(x \in \mathbf{R} \backslash\left\{\frac{\pi}{2} + k\pi: k \in \mathbf{Z}\right\}\).

Przekształcamy lewą stronę: \[L=\frac{1+2 \sin x \cos x}{\cos ^{2} x}\] Stosujemy wzór na jedynkę trygonometryczną: \[ \begin{split} &L=\frac{\sin^2 x + \cos^2 x + 2\sin x \cos x}{\cos^2 x}=\\[6pt] &=\frac{(\sin x+\cos x)^2}{\cos^2 x}=\\[6pt] &=\left(\frac{\sin x+\cos x}{\cos x}\right)^2=\\[6pt] &=\left(\frac{\sin x}{\cos x}+\frac{\cos x}{\cos x}\right)^2=\\[6pt] &=\left(\operatorname{tg} x + 1\right)^2 \end{split} \] Otrzymaliśmy dokładnie prawą stronę: \[P=(1+\operatorname{tg} x)^2\] Zatem zachodzi równość \(L = P\).

Udowodnij tożsamość: \(\frac{\operatorname{tg} x+\cos x}{\cos x \sin x}=\frac{1}{\sin x}+\frac{1}{\cos ^{2} x}\).

Zakładamy, że wyrażenie jest określone, czyli, że: \(\sin x \ne 0\) oraz \(\cos x \ne 0\). Tak jest dla \(x \in \mathbf{R} \backslash\left\{\frac{k\pi}{2}: k \in \mathbf{Z}\right\}\).

Przekształcamy lewą stronę: \[ L=\frac{\operatorname{tg} x+\cos x}{\cos x \sin x} \] Stosujemy wzór na tangens \(\operatorname{tg} x = \frac{\sin x}{\cos x}\): \[ \begin{split} &L=\frac{\frac{\sin x}{\cos x}+\cos x}{\cos x \sin x}=\\[6pt] &=\frac{\frac{\sin x}{\cos x}}{\cos x \sin x}+\frac{\cos x}{\cos x \sin x}=\\[6pt] &=\frac{1}{\cos^2 x} + \frac{1}{\sin x}=P \end{split} \] Zatem zachodzi równość \(L = P\).

Udowodnij tożsamość: \(\frac{\cos x}{1-\sin x}+\frac{\cos x}{1+\sin x}=\frac{2}{\cos x}\).

Zakładamy, że wyrażenie jest określone, czyli, że: \(\cos x \ne 0\) oraz \(1-\sin x \ne 0\) oraz \(1+\sin x \ne 0\). Tak jest dla \(x \in \mathbf{R} \backslash\left\{\frac{\pi}{2} + k\pi: k \in \mathbf{Z}\right\}\).

Przekształcamy lewą stronę: \[ L = \frac{\cos x}{1-\sin x}+\frac{\cos x}{1+\sin x} \] Sprowadzamy do wspólnego mianownika: \[ (1-\sin x)(1+\sin x) = 1 - \sin^2 x = \cos^2 x \] Rozpisujemy ułamki: \[ \begin{split} &L = \frac{\cos x (1+\sin x) + \cos x (1-\sin x)}{(1-\sin x)(1+\sin x)}=\\[6pt] &=\frac{\cos x + \cos x \sin x + \cos x - \cos x \sin x}{\cos^2 x}=\\[6pt] &=\frac{2\cos x}{\cos^2 x}=\frac{2}{\cos x}=P \end{split} \] Zatem zachodzi równość \(L = P\).

Udowodnij tożsamość: \(\frac{\operatorname{tg} x}{\operatorname{tg} x+\operatorname{ctg} x}=\sin ^{2} x\).

Zakładamy, że wyrażenie jest określone, czyli, że: \(\sin x \ne 0\) oraz \(\cos x \ne 0\) oraz \(\operatorname{tg} x+\operatorname{ctg} x \ne 0\). Tak jest dla \(x \in \mathbf{R} \backslash\left\{\frac{k\pi}{2}: k \in \mathbf{Z}\right\}\).

Przekształcamy lewą stronę: \[ L = \frac{\operatorname{tg} x}{\operatorname{tg} x+\operatorname{ctg} x} \] Stosujemy wzory na tangens i cotangens: \[ \operatorname{tg} x = \frac{\sin x}{\cos x}, \quad \operatorname{ctg} x = \frac{\cos x}{\sin x} \] Podstawiamy do wyrażenia: \[ \begin{split} &L = \frac{\frac{\sin x}{\cos x}}{\frac{\sin x}{\cos x} + \frac{\cos x}{\sin x}}=\\[6pt] &=\frac{\frac{\sin x}{\cos x}}{\frac{\sin^2 x + \cos^2 x}{\cos x \sin x}}=\\[6pt] &=\frac{\frac{\sin x}{\cos x}}{\frac{1}{\cos x \sin x}}=\\[6pt] &=\frac{\sin x}{\cos x} \cdot \frac{\cos x \sin x}{1}=\\[6pt] &=\sin^2 x=P \end{split} \] Zatem zachodzi równość \(L = P\).

Udowodnij tożsamość: \(\frac{\operatorname{tg} x\left(1+\operatorname{ctg}^{2} x\right)}{1+\operatorname{tg}^{2} x}=\frac{1-\sin ^{2} x}{\sin x \cos x}\).

Zakładamy, że wyrażenie jest określone, czyli, że: \(\sin x \ne 0\) oraz \(\cos x \ne 0\). Tak jest dla \(x \in \mathbf{R} \backslash\left\{\frac{k \pi}{2}: k \in \mathbf{Z}\right\}\).

Przekształcamy lewą stronę: \[L=\frac{\operatorname{tg} x\left(1+\operatorname{ctg}^2 x\right)}{1+\operatorname{tg}^2 x}\] Stosujemy wzory na tangens i cotangens: \[ \begin{split} &L=\frac{\operatorname{tg} x\left(1+\operatorname{ctg}^2 x\right)}{1+\operatorname{tg}^2 x}=\\[16pt] &=\frac{\frac{\sin x}{\cos x}\left(1+\left(\frac{\cos x}{\sin x}\right)^2\right)}{1+\left(\frac{\sin x}{\cos x}\right)^2}=\\[16pt] &=\frac{\frac{\sin x}{\cos x}\left(\frac{\sin^2 x + \cos^2 x}{\sin^2 x}\right)}{\frac{\cos^2 x + \sin^2 x}{\cos^2 x}}=\\[16pt] &=\frac{\frac{\sin x}{\cos x}\left(\frac{1}{\sin^2 x}\right)}{\frac{1}{\cos^2 x}}=\\[16pt] &=\frac{\sin x}{\cos x\sin^2 x} \cdot \cos^2 x=\\[16pt] &=\frac{\cos x}{\sin x} \end{split}\] Przekształcamy prawą stronę: \[P=\frac{1-\sin^2 x}{\sin x \cos x}\] Stosujemy tożsamość \(\sin^2 x + \cos^2 x = 1\): \[ \begin{split} &P=\frac{1-\sin^2 x}{\sin x \cos x}=\\[16pt] &=\frac{\cos^2 x}{\sin x \cos x}=\\[16pt] &=\frac{\cos x}{\sin x} \end{split}\] Zatem zachodzi równość \(L = P\).

Udowodnij tożsamość: \(\frac{\operatorname{tg} x-\operatorname{ctg} x}{\operatorname{tg} x+\operatorname{ctg} x}=\frac{\operatorname{tg}^{2} x-1}{\operatorname{tg}^{2} x+1}\).

Zakładamy, że wyrażenie jest określone, czyli, że: \(\sin x \ne 0\) oraz \(\cos x \ne 0\) (to są mianowniki tangensa i cotangensa). Tak jest dla \(x \in \mathbf{R} \backslash\left\{\frac{k \pi}{2}: k \in \mathbf{Z}\right\}\).

Przekształcamy lewą stronę: \[L=\frac{\operatorname{tg} x - \operatorname{ctg} x}{\operatorname{tg} x + \operatorname{ctg} x}\] Stosujemy wzory na tangens i cotangens: \[ \begin{split} L &= \frac{\frac{\sin x}{\cos x} - \frac{\cos x}{\sin x}}{\frac{\sin x}{\cos x} + \frac{\cos x}{\sin x}}= \\[16pt] &= \frac{\frac{\sin^2 x - \cos^2 x}{\cos x \sin x}}{\frac{\sin^2 x + \cos^2 x}{\cos x \sin x}}= \\[16pt] &= \frac{\sin^2 x - \cos^2 x}{\sin^2 x + \cos^2 x}= \\[16pt] &= \frac{\sin^2 x - \cos^2 x}{1}= \\[12pt] &=\sin^2 x - \cos^2 x \end{split} \] Przekształcamy prawą stronę: \[P=\frac{\operatorname{tg}^{2} x - 1}{\operatorname{tg}^{2} x + 1}\] Używając wzoru \(\operatorname{tg}^{2} x = \frac{\sin^2 x}{\cos^2 x}\): \[ \begin{split} P &= \frac{\frac{\sin^2 x}{\cos^2 x} - 1}{\frac{\sin^2 x}{\cos^2 x} + 1}= \\[16pt] &= \frac{\frac{\sin^2 x - \cos^2 x}{\cos^2 x}}{\frac{\sin^2 x + \cos^2 x}{\cos^2 x}} =\\[16pt] &= \frac{\sin^2 x - \cos^2 x}{\sin^2 x + \cos^2 x}= \\[16pt] &= \frac{\sin^2 x - \cos^2 x}{1}= \\[12pt] &=\sin^2 x - \cos^2 x \end{split} \] Zatem zachodzi równość \(L = P\).

Udowodnij tożsamość: \(\frac{\operatorname{ctg} x\cdot (1+\operatorname{tg} ^2x)}{1+\operatorname{ctg} ^2x}=\operatorname{tg} x\).

Zakładamy, że wyrażenie jest określone, czyli, że: \(\sin x \ne 0\) oraz \(\cos x \ne 0\) (mianowniki tangensa i cotangensa muszą być różne od zera). Tak jest dla \(x \in \mathbf{R} \backslash\left\{\frac{k \pi}{2}: k \in \mathbf{Z}\right\}\).

Przekształcamy lewą stronę: \[L=\frac{\operatorname{ctg} x \cdot (1+\operatorname{tg}^2 x)}{1+\operatorname{ctg}^2 x}\] Stosujemy wzory na tangens i cotangens: \[ \begin{split} L &= \frac{\frac{\cos x}{\sin x} \cdot \left(1+\left(\frac{\sin x}{\cos x}\right)^2\right)}{1+\left(\frac{\cos x}{\sin x}\right)^2} \\[16pt] &= \frac{\frac{\cos x}{\sin x} \cdot \left(\frac{\cos^2 x + \sin^2 x}{\cos^2 x}\right)}{\frac{\sin^2 x + \cos^2 x}{\sin^2 x}} \\[16pt] &= \frac{\frac{\cos x}{\sin x} \cdot \frac{1}{\cos^2 x}}{\frac{1}{\sin^2 x}} \\[16pt] &= \frac{\cos x}{\sin x \cos^2 x} \cdot \sin^2 x \\[16pt] &= \frac{\sin x}{\cos x} \end{split} \] Przekształcamy prawą stronę: \[P=\operatorname{tg} x\] Stosujemy wzór na tangens: \[ \begin{split} P &= \frac{\sin x}{\cos x} \end{split} \] Zatem zachodzi równość \(L = P\).