Metoda graficzna

Poziom podstawowy

Układ dwóch równań liniowych z dwiema niewiadomymi, to układ, który można zapisać w postaci: \[\begin{cases} y=ax+b\\ y=cx+d \end{cases}\] gdzie \(a, b, c, d\) - to współczynniki liczbowe.

Taki układ równań można czasem rozwiązać metodą graficzną (stosując interpretację geometryczną układu równań). W tym celu rysujemy w układzie współrzędnych obie proste i punkt ich przecięcia (o ile istnieje) jest rozwiązaniem układu równań.

Precyzyjne odczytanie takiego rozwiązania jest możliwe właściwie tylko wtedy, gdy punkt przecięcia prostych przypada na punkt kratowy układu współrzędnych.
Z tego względu ta metoda jest stosowana głównie jako pomocnicza, w sytuacji gdy i tak musimy narysować proste w układzie współrzędnych. Wówczas przy dokładnym rysunku możemy uzyskać współrzędne punktu przecięcia prostych, bez rozwiązywania układu równań.

Znajdź rozwiązanie układu równań metodą graficzną: \[\begin{cases} x+2y=8\\ 2x-y=1 \end{cases} \]

Przekształcamy oba równania do postaci \(y=ax+b\): \[\begin{split} &\begin{cases} 2y=-x+8\\ -y=-2x+1 \end{cases} \\[16pt] &\begin{cases} y=-\frac{1}{2}x+4\\ y=2x-1 \end{cases} \\ \end{split} \]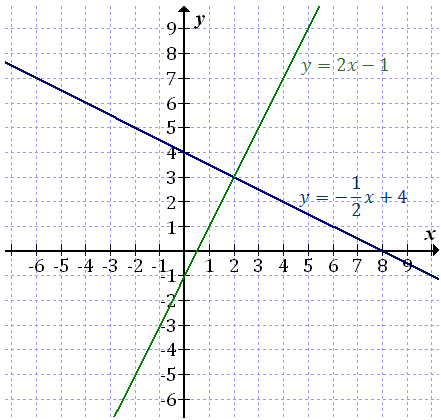

A następnie rysujemy wykresy obu funkcji i odczytujemy punkt przecięcia:

Zatem rozwiązaniem układu równań jest para liczb: \[\begin{cases} x=2\\ y=3 \end{cases} \]

Na rysunku przedstawiono geometryczną interpretację jednego z niżej zapisanych układów równań.

Wskaż ten układ.

A.\(\begin{cases} {y=x-1}\\ {y=-2x+4} \end{cases} \)

B.\(\begin{cases} {y=x-1}\\ {y=2x+4} \end{cases} \)

C.\(\begin{cases} {y=x+1}\\ {y=-2x+4} \end{cases} \)

D.\(\begin{cases} {y=x+1}\\ {y=2x+4} \end{cases} \)

Na jednym z poniższych rysunków przedstawiono interpretację geometryczną układu równań \[\begin{cases} x+3y=-5 \\ 3x-2y=-4 \end{cases} \] Wskaż ten rysunek.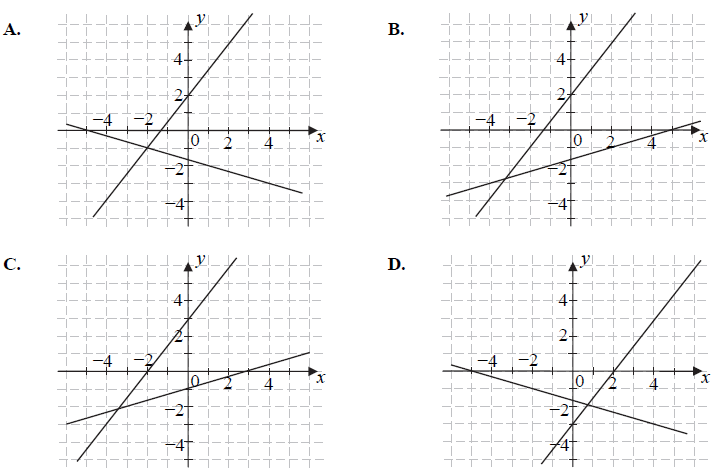

Na rysunku jest przedstawiona graficzna ilustracja układu dwóch równań stopnia pierwszego z dwiema niewiadomymi \(x\) i \(y.\)

wskaż ten układ.

A.\( \begin{cases} y=-2x+8 \\ y=-\frac{3}{2}x+\frac{13}{2} \end{cases} \)

B.\( \begin{cases} y=2x-4 \\ y=-\frac{1}{2}x+\frac{7}{2} \end{cases} \)

C.\( \begin{cases} y=x-1 \\ y=\frac{1}{2}x+\frac{1}{2} \end{cases} \)

D.\( \begin{cases} y=3x-7 \\ y=-\frac{2}{3}x+4 \end{cases} \)

Na rysunku obok przedstawiono geometryczną interpretację jednego z niżej zapisanych układów równań. Wskaż ten układ, którego geometryczną interpretację przedstawiono na rysunku.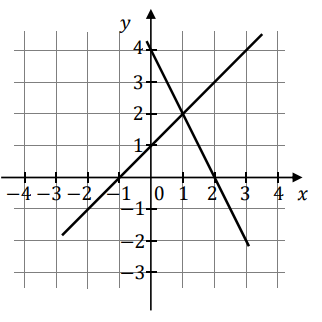

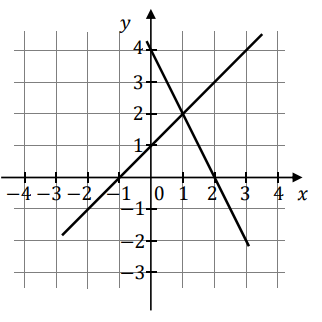
A.\( \begin{cases} y=x+1 \\ y=-2x+4 \end{cases} \)

B.\( \begin{cases} y=x-1 \\ y=2x+4 \end{cases} \)

C.\( \begin{cases} y=x-1 \\ y=-2x+4 \end{cases} \)

D.\( \begin{cases} y=x+1 \\ y=2x+4 \end{cases} \)

Na rysunku przedstawiono interpretację geometryczną w kartezjańskim układzie współrzędnych \((x,y)\) jednego z niżej zapisanych układów równań A–D.

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Układem równań, którego interpretację geometryczną przedstawiono na rysunku, jest

A.\( \begin{cases} y=-x+2 \\ y=-2x+1 \end{cases} \)

B.\( \begin{cases} y=x-2 \\ y=-2x-1 \end{cases} \)

C.\( \begin{cases} y=x-2 \\ y=2x+1 \end{cases} \)

D.\( \begin{cases} y=-x+2 \\ y=2x-1 \end{cases} \)

Na rysunku, w kartezjańskim układzie współrzędnych \((x, y)\), przedstawiono dwie proste równoległe, które są interpretacją geometryczną jednego \(z\) poniższych układów równań A-D.

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Układem równań, którego interpretację geometryczną przedstawiono na rysunku, jest

A.\(\left\{\begin{array}{l}y=-\frac{3}{2} x+3 \\ y=-\frac{3}{2} x-1\end{array}\right.\)

B.\(\left\{\begin{array}{l}y=\frac{3}{2} x+3 \\ y=-\frac{2}{3} x-1\end{array}\right.\)

C.\(\left\{\begin{array}{l}y=\frac{3}{2} x+3 \\ y=\frac{3}{2} x-1\end{array}\right.\)

D.\(\left\{\begin{array}{l}y=-\frac{3}{2} x-3 \\ y=\frac{3}{2} x+1\end{array}\right.\)