Matura rozszerzona - zbiór zadań - zadania dowodowe geometryczne
Poziom rozszerzony
Dany jest trójkąt równoramienny \(ABC\), w którym \(|AC|=|BC|=6\), a punkt \(D\) jest środkiem podstawy \(AB\). Okrąg o środku \(D\) jest styczny do prostej \(AC\) w punkcie \(M\). Punkt \(K\) leży na boku \(AC\), punkt \(L\) leży na boku \(BC\), odcinek \(KL\) jest styczny do rozważanego okręgu oraz \(|KC|=|LC|=2\) (zobacz rysunek).  Wykaż, że \(\frac{|AM|}{|MC|}=\frac{4}{5}\).
Wykaż, że \(\frac{|AM|}{|MC|}=\frac{4}{5}\).
 Wykaż, że \(\frac{|AM|}{|MC|}=\frac{4}{5}\).
Wykaż, że \(\frac{|AM|}{|MC|}=\frac{4}{5}\).Okrąg \(\mathcal{O}\) jest styczny do boków \(A C\) i \(B C\) trójkąta \(A B C\) oraz przecina bok \(A B\) tego trójkąta w punktach \(M\) oraz \(N\), przy czym \(0\lt |A M|\lt |A N|\lt |A B|\).
Wykaż, że jeśli \(|A M|=|B N|\), to trójkąt \(A B C\) jest równoramienny.
Dany jest okrąg \(O\). Przez punkt \(A\) poprowadzono dwie proste, które są styczne do tego okręgu w punktach - odpowiednio - \(P\) oraz \(Q\). Przez punkt \(B\) leżący na odcinku \(AP\) poprowadzono styczną do tego okręgu w punkcie \(D\), która przecięła odcinek \(AQ\) w punkcie \(C\) (zobacz rysunek). 

Wykaż, że jeżeli \(|AQ|=5\cdot |BP|\) oraz \(|CD|=2\cdot |BD|\), to trójkąt \(ABC\) jest równoramienny.
Punkt \(E\) jest środkiem boku \(BC\) prostokąta \(ABCD\), w którym \(AB>BC\). Punkt \(F\) leży na boku \(CD\) tego prostokąta oraz \(\sphericalangle AEF=90^\circ \). Udowodnij, że \(\sphericalangle BAE=\sphericalangle EAF\).
W trójkącie ostrokątnym \(ABC\) bok \(AB\) ma długość \(c\), długość boku \(BC\) jest równa \(a\) oraz \(|\sphericalangle ABC|=\beta \). Dwusieczna kąta \(ABC\) przecina bok \(AC\) trójkąta w punkcie \(E\). Wykaż, że długość odcinka \(BE\) jest równa \(\frac{2ac \cdot \cos \frac{\beta }{2}}{a+c}\).
Trójkąt \(ABC\) jest ostrokątny oraz \(|AC| \gt | BC|\). Dwusieczna \(d_C\) kąta \(ACB\) przecina bok \(AB\) w punkcie \(K\). Punkt \(L\) jest obrazem punktu \(K\) w symetrii osiowej względem dwusiecznej \(d_A\) kąta \(BAC\), punkt \(M\) jest obrazem punktu \(L\) w symetrii osiowej względem dwusiecznej \(d_C\) kąta \(ACB\), a punkt \(N\) jest obrazem punktu \(M\) w symetrii osiowej względem dwusiecznej \(d_B\) kąta \(ABC\) (zobacz rysunek).  Udowodnij, że na czworokącie \(KNML\) można opisać okrąg.
Udowodnij, że na czworokącie \(KNML\) można opisać okrąg.
 Udowodnij, że na czworokącie \(KNML\) można opisać okrąg.
Udowodnij, że na czworokącie \(KNML\) można opisać okrąg.W trójkącie \(ABC\): \(|AB|=c\), \(|AC|=b\), \(|BC|=a\) oraz \(|\sphericalangle BAC|=\alpha \) i \(|\sphericalangle ABC|=\beta \) (zobacz rysunek). Wykaż, że jeżeli \(\alpha =2\beta \), to \(a^2-b^2=bc\). 

Dany jest trójkąt równoramienny \(ABC\), w którym \(|AC| = |BC|\). Na ramieniu \(AC\) tego trójkąta wybrano punkt \(M (M \ne A\) i \(M \ne C)\), a na ramieniu \(BC\) wybrano punkt \(N\), w taki sposób, że \(|AM| = |CN|\). Przez punkty \(M\) i \(N\) poprowadzono proste prostopadłe do podstawy \(AB\) tego trójkąta, które wyznaczają na niej punkty \(S\) i \(T\). Udowodnij, że \(|ST| = \frac{1}{2}|AB|\).
Dany jest trójkąt prostokątny o przyprostokątnych długości \(a\) i \(b\), w którym kąt między środkową a wysokością wychodzącymi z wierzchołka kąta prostego ma miarę \(\alpha \). Wykaż, że \(\operatorname{tg} \alpha =\frac{|a^2-b^2|}{2ab}\).
Dany jest trójkąt równoboczny \(ABC\). Na bokach \(AB\) i \(AC\) wybrano punkty – odpowiednio – \(D\) i \(E\) takie, że \(|BD| = |AE| = \frac{1}{3}|AB|\). Odcinki \(CD\) i \(BE\) przecinają się w punkcie \(P\) (zobacz rysunek).  Wykaż, że pole trójkąta \(DBP\) jest \(21\) razy mniejsze od pola trójkąta \(ABC\).
Wykaż, że pole trójkąta \(DBP\) jest \(21\) razy mniejsze od pola trójkąta \(ABC\).
 Wykaż, że pole trójkąta \(DBP\) jest \(21\) razy mniejsze od pola trójkąta \(ABC\).
Wykaż, że pole trójkąta \(DBP\) jest \(21\) razy mniejsze od pola trójkąta \(ABC\).Punkt \(P\) jest punktem przecięcia przekątnych trapezu \(ABCD\). Długość podstawy \(CD\) jest o \(2\) mniejsza od długości podstawy \(AB\). Promień okręgu opisanego na trójkącie ostrokątnym \(CPD\) jest o \(3\) mniejszy od promienia okręgu opisanego na trójkącie \(APB\). Wykaż, że spełniony jest warunek \(|DP|^2+|CP|^2-|CD|^2=\frac{4\sqrt{2}}{3}\cdot |DP|\cdot |CP|\).
Dany jest trójkąt prostokątny \(ABC\), w którym \(|\sphericalangle ABC| = 90^\circ\) oraz \(|\sphericalangle CAB| = 60^\circ\). Punkty \(K\) i \(L\) leżą na bokach - odpowiednio - \(AB\) i \(BC\) tak, że \(|BK| = |BL| = 1\) (zobacz rysunek). Odcinek \(KL\) przecina wysokość \(BD\) tego trójkąta w punkcie \(N\), a ponadto \(|AD| = 2\). 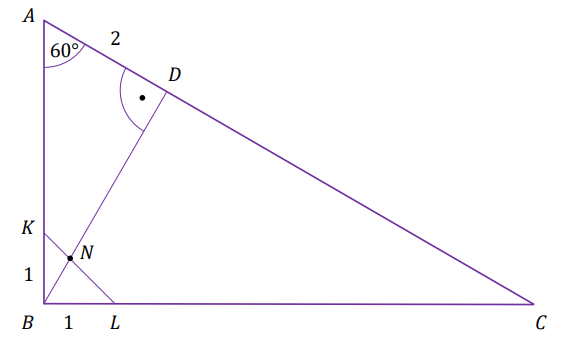

Wykaż, że \(|ND|=\sqrt{3}+1\).
Trójkąt \(ABC\), w którym \(|AC| = |BC|\), jest wpisany w okrąg o promieniu \(R\). Środek tego okręgu leży wewnątrz trójkąta \(ABC\). Niech \(x\) oznacza odległość środka okręgu od podstawy \(AB\).
Wykaż, że pole trójkąta \(ABC\) jako funkcja zmiennej \(x\) jest określone wzorem \(P(x)=(R+x)\sqrt{R^2-x^2}\). Określ dziedzinę tej funkcji.
Na przeciwprostokątnej \(AB\) trójkąta prostokątnego \(ABC\) zbudowano kwadrat \(ABDE\) (zobacz rysunek). Stosunek pola trójkąta do pola kwadratu jest równy \(k\). Wykaż, że suma tangensów kątów ostrych tego trójkąta jest równa \(\frac{1}{2k}\). 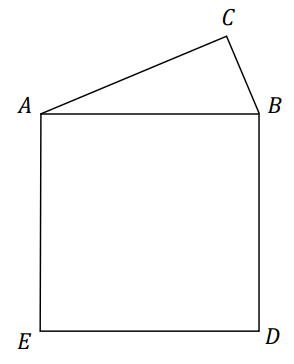

W trójkącie ostrokątnym \(ABC\) miara kąta \(BAC\) jest dwa razy większa od miary kąta \(ABC\). Punkt \(D\) jest środkiem boku \(AB\). Niech \(\alpha\) oznacza miarę kąta \(ABC\), natomiast \(\beta\)-miarę kąta \(ADC\) (zobacz rysunek). 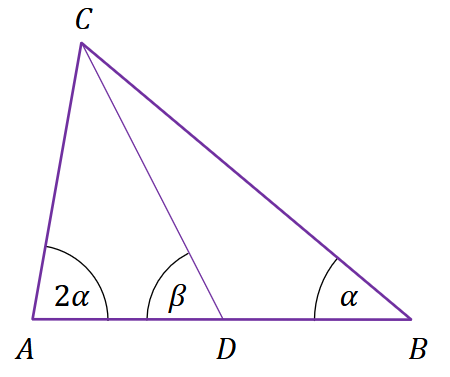

Oblicz \(\frac{\operatorname{tg} \beta}{\sin (2 \alpha)}\). Zapisz obliczenia.
W pięciokącie wypukłym \(A B C D E\) połączono środki boków \(A B\) i \(D C\) odcinkiem \(K L\) oraz środki boków \(B C\) i \(D E\) odcinkiem \(M N\) (zobacz rysunek). Punkty \(P\) i \(Q\) są środkami odcinków odpowiednio \(K L\) i \(M N\). 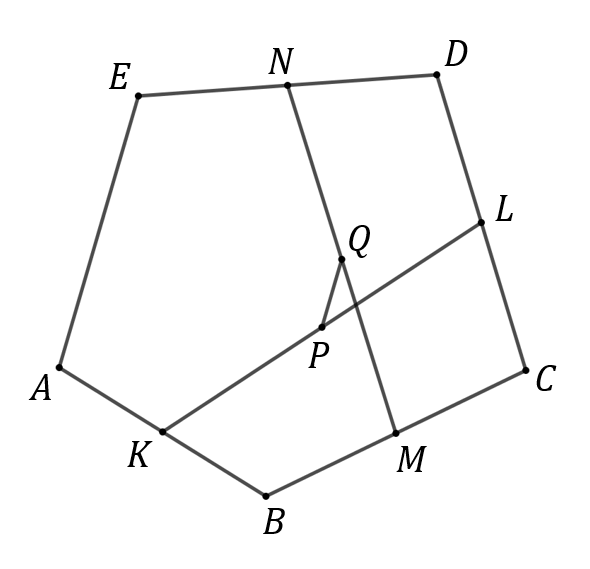

Wykaż, że \(P Q \| A E\) i \(|P Q|=0,25|A E|\).
Tematy nadrzędne