Matura rozszerzona - zbiór zadań - wzory i zależności trygonometryczne
Poziom rozszerzony
Wykaż, że \[\frac{1+2\cos 88^\circ \cdot \cos 2^\circ }{\cos^22^\circ -\cos 88^\circ \cdot \sin 2^\circ }=\frac{1+\operatorname{tg} 2^\circ }{1-\operatorname{tg} 2^\circ }\]
Na płaszczyźnie, w kartezjańskim układzie współrzędnych \((x, y)\), dane są dwie proste \(l_1\) oraz \(l_2\). Kąt między tymi prostymi ma miarę \(45^\circ\). Współczynnik kierunkowy w równaniu prostej \(l_1\) jest równy \(\frac{2}{3}\).
Oblicz współczynnik kierunkowy w równaniu prostej \(l_2\). Zapisz obliczenia.
Na szczycie wieży o wysokości \(h\) umieszczono pionowo antenę radiową stacji nadawczej o długości \(l\) (\(l\gt h\)). Punkt \(O\) leży na płaszczyźnie poziomej przechodzącej przez podnóże wieży, a punkt \(A\) znajduje się na końcu anteny. Koniec anteny \(A\) widać z punktu \(O\) pod dwukrotnie większym kątem niż wieżę (zobacz rysunek). 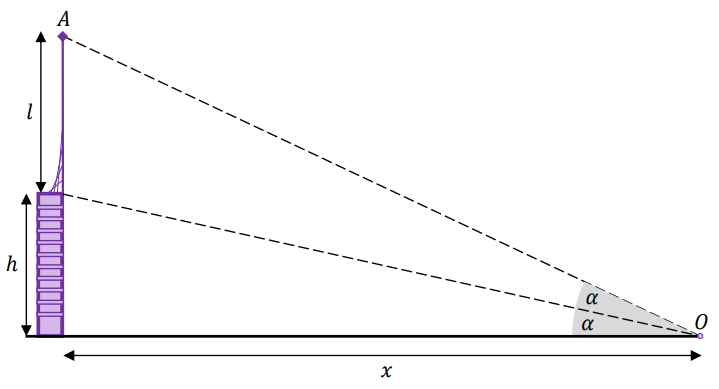

Oblicz odległość \(x\) podnóża wieży od punktu \(O\). Zapisz obliczenia.