Matura rozszerzona - zbiór zadań - twierdzenie sinusów i cosinusów
Poziom rozszerzony
W trójkącie \(ABC\) bok \(AB\) jest \(3\) razy dłuższy od boku \(AC\), a długość boku \(BC\) stanowi \(\frac{4}{5}\) długości boku \(AB\). Oblicz cosinus najmniejszego kąta trójkąta \(ABC\). W kratki poniżej wpisz kolejno – od lewej do prawej – pierwszą, drugą oraz trzecią cyfrę po przecinku nieskończonego rozwinięcia dziesiętnego otrzymanego wyniku.
Na boku \(AB\) trójkąta \(ABC\) obrano punkty \(D\) i \(E\) takie, że \(|AD|=|EB|=\frac{1}{4}|AB|\) (zobacz rysunek). Udowodnij, że \(|AC|^2+2|CE|^2=|BC|^2+2|CD|^2\). 

Trójkąt o boku \(a\) i kącie ostrym \(\alpha \), leżącym naprzeciw tego boku, jest wpisany w okrąg o promieniu \(R\), zaś trójkąt o boku \(a+1\) i kącie ostrym \(\alpha \), leżącym naprzeciw tego boku, jest wpisany w okrąg o promieniu \(R+1\). Wyznacz miarę kąta \(\alpha \).
Czworokąt \(ABCD\) jest wpisany w okrąg o promieniu \(R=5\sqrt{2}\). Przekątna \(BD\) tego czworokąta ma długość \(10\). Kąty wewnętrzne \(BAD\) i \(ADC\) czworokąta \(ABCD\) są ostre, a iloczyn sinusów wszystkich jego kątów wewnętrznych jest równy \(\frac{3}{8}\). Oblicz miary kątów wewnętrznych tego czworokąta.
Dany jest trójkąt prostokątny \(ABC\). Promień okręgu wpisanego w ten trójkąt jest pięć razy krótszy od przeciwprostokątnej tego trójkąta. Oblicz sinus tego z kątów ostrych trójkąta \(ABC\), który ma większą miarę.
Długości boków czworokąta \(ABCD\) są równe: \(|AB|=2, |BC|=3, |CD|=4, |DA|=5\). Na czworokącie \(ABCD\) opisano okrąg. Oblicz długość przekątnej \(AC\) tego czworokąta.
Punkt \(D\) leży na boku \(AB\) trójkąta \(ABC\) oraz \(|AC| = 16\), \(|AD| = 6\), \(|CD| = 14\) i \(|BC| = |BD|\). Oblicz obwód trójkąta \(ABC\).
Dany jest graniastosłup prosty \(ABCDEFGH\) o podstawie prostokątnej \(ABCD\). Przekątne \(AH\) i \(AF\) ścian bocznych tworzą kąt ostry o mierze \(\alpha \) takiej, że \(\sin \alpha =\frac{12}{13}\) (zobacz rysunek). Pole trójkąta \(AFH\) jest równe \(26{,}4\). Oblicz wysokość \(h\) tego graniastosłupa. 

W trójkącie \(ABC\) są dane \(|AB|=8\), \(|BC|=6\) oraz \(\sin \sphericalangle ABC=\frac{\sqrt{5}}{3}\). Oblicz stosunek promienia okręgu opisanego na trójkącie \(ABC\) do promienia okręgu wpisanego w ten trójkąt.
W pewien okrąg wpisano czworokąt \(ABCD\) taki, że \(|AB| = 10\), \(|CD| = 6\) oraz \(|BC| = |BD|\). Styczna do tego okręgu w punkcie \(C\) tworzy z bokiem \(CD\) kąt \(\alpha\) o mierze \(30^\circ\) (zobacz rysunek). 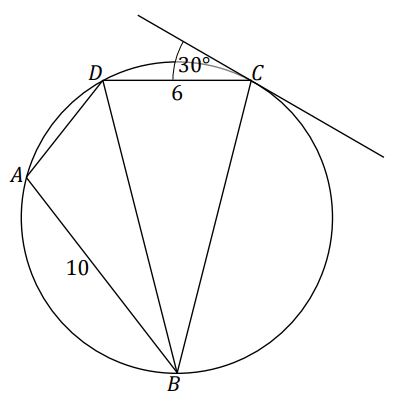

Oblicz pole czworokąta \(ABCD\). Zapisz obliczenia.
Tematy nadrzędne