Matura rozszerzona - zbiór zadań - prosta i parabola

Drukuj

Poziom rozszerzony

Napisz równania wszystkich prostych, które są jednocześnie styczne do paraboli o równaniu \(y=\frac{1}{4}x^2-1\) i do okręgu o równaniu \(x^2+(y+6)^2=8\).

\(y=x-2, y=-x-2, y=\sqrt{17}x-18,y=-\sqrt{17}x-18\)

W kartezjańskim układzie współrzędnych \((x, y)\) prosta \(l\) o równaniu \(x - y - 2 = 0\) przecina parabolę o równaniu \(y = 4x^2 - 7x + 1\) w punktach \(A\) oraz \(B\). Odcinek \(AB\) jest średnicą okręgu \(O\). Punkt \(C\) leży na okręgu \(O\) nad prostą \(l\), a kąt \(BAC\) jest ostry i ma miarę \(\alpha\) taką, że \(\operatorname{tg} \alpha = \frac{1}{3}\) (zobacz rysunek).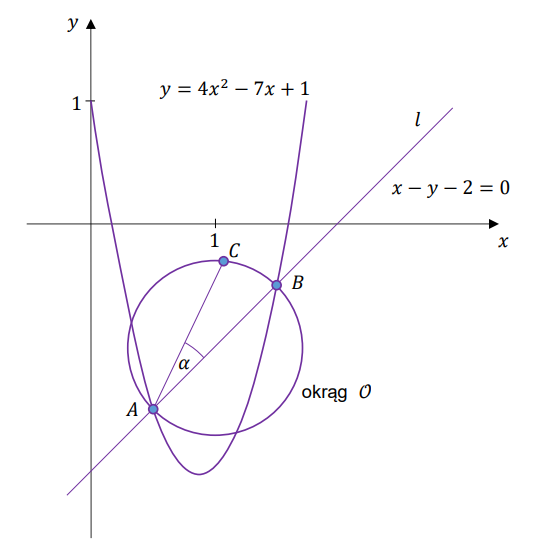

Oblicz współrzędne punktu \(C\). Zapisz obliczenia.

\(C=\left(\frac{11}{10}, -\frac{3}{10}\right)\)

Dane są parabola o równaniu \(y=x^2\) oraz punkty \(A = (0, 2)\) i \(B = (1, 3)\) (zobacz rysunek). Rozpatrujemy wszystkie trójkąty \(ABC\), których wierzchołek \(C\) leży na tej paraboli. Niech \(m\) oznacza pierwszą współrzędną punktu \(C\).

Wyznacz pole \(P\) trójkąta \(ABC\) jako funkcję zmiennej \(m\).

Wyznacz wszystkie wartości \(m\), dla których trójkąt \(ABC\) jest ostrokątny.