Matura rozszerzona - zbiór zadań - podobieństwo figur
Poziom rozszerzony
Dany jest trójkąt równoramienny \(ABC\), w którym \(|AC|=|BC|=6\), a punkt \(D\) jest środkiem podstawy \(AB\). Okrąg o środku \(D\) jest styczny do prostej \(AC\) w punkcie \(M\). Punkt \(K\) leży na boku \(AC\), punkt \(L\) leży na boku \(BC\), odcinek \(KL\) jest styczny do rozważanego okręgu oraz \(|KC|=|LC|=2\) (zobacz rysunek).  Wykaż, że \(\frac{|AM|}{|MC|}=\frac{4}{5}\).
Wykaż, że \(\frac{|AM|}{|MC|}=\frac{4}{5}\).
 Wykaż, że \(\frac{|AM|}{|MC|}=\frac{4}{5}\).
Wykaż, że \(\frac{|AM|}{|MC|}=\frac{4}{5}\).Z wierzchołków kwadratu poprowadzono do odpowiednich boków proste pod takim samym kątem \(\alpha \), mniejszym od \(45^\circ \), (zobacz rysunek). Proste te wyznaczają w szczególności trójkąt (zacieniowany) o polu \(9\) i czworokąt (zacieniowany) o polu \(7\). Wyznacz pole kwadratu. 

Na podstawie \(AB\) trapezu \(ABCD\) (\(|AB|\gt |CD|\)) wyznaczono taki punkt \(E\), że czworokąt \(AECD\) jest równoległobokiem. Przekątna \(BD\) przecina odcinki \(CA\) i \(CE\) odpowiednio w punktach \(F\) i \(G\). Odcinki \(DG\) i \(BF\) są równej długości. Uzasadnij, że \(\frac{|AB|}{|CD|}=\frac{1+\sqrt{5}}{2}\). 

Dany jest prostokąt \(ABCD\). Okrąg wpisany w trójkąt \(BCD\) jest styczny do przekątnej \(BD\) w punkcie \(N\). Okrąg wpisany w trójkąt \(ABD\) jest styczny do boku \(AD\) w punkcie \(M\), a środek \(S\) tego okręgu leży na odcinku \(MN\), jak na rysunku.  Wykaż, że \(|MN|=|AD|\).
Wykaż, że \(|MN|=|AD|\).
 Wykaż, że \(|MN|=|AD|\).
Wykaż, że \(|MN|=|AD|\).Dany jest trójkąt równoboczny \(ABC\). Na bokach \(AB\) i \(AC\) wybrano punkty – odpowiednio – \(D\) i \(E\) takie, że \(|BD| = |AE| = \frac{1}{3}|AB|\). Odcinki \(CD\) i \(BE\) przecinają się w punkcie \(P\) (zobacz rysunek).  Wykaż, że pole trójkąta \(DBP\) jest \(21\) razy mniejsze od pola trójkąta \(ABC\).
Wykaż, że pole trójkąta \(DBP\) jest \(21\) razy mniejsze od pola trójkąta \(ABC\).
 Wykaż, że pole trójkąta \(DBP\) jest \(21\) razy mniejsze od pola trójkąta \(ABC\).
Wykaż, że pole trójkąta \(DBP\) jest \(21\) razy mniejsze od pola trójkąta \(ABC\).W trapezie \(ABCD\) przekątna \(BD\) jest dwusieczną kąta \(CBA\) i przecina przekątną \(AC\) w punkcie \(K\), takim, że \(|CK|:|KA| = 1 : 3\). Pole tego trapezu jest równe \(100(\sqrt{6}-\sqrt{2})\), \(\sin\sphericalangle BAD=\frac{\sqrt{6}+\sqrt{2}}{4}\), \(|AD| = 10\) oraz kąt \(BAD\) jest ostry.
Oblicz długości pozostałych boków trapezu \(ABCD\). Zapisz obliczenia.
Czworokąt wypukły \(ABCD\) jest wpisany w okrąg o promieniu \(4\). Kąty \(BAD\) i \(BCD\) są proste (zobacz rysunek). Przekątne \(AC\) i \(BD\) tego czworokąta przecinają się w punkcie \(E\) tak, że \(|BE| = 3\cdot |DE|\) oraz \(|BD| = 2\cdot |AE|\). 

Oblicz długości boków czworokąta \(ABCD\). Zapisz obliczenia.
Dane są punkty: \(A=(-1,-2), B=(1,4), C=(-2,-10), D=(2,2)\). Wykaż, że odcinki \(AB\) i \(CD\) są równoległe. Wyznacz środek jednokładności \(S\) i dodatnią skalę \(k\) tak, aby obrazem odcinka \(AB\) w tej jednokładności był odcinek \(CD\).
Prosta o równaniu \(x+y-10=0\) przecina okrąg o równaniu \(x^2+y^2-8x-6y+8=0\) w punktach \(K\) i \(L\). Punkt \(S\) jest środkiem cięciwy \(KL\). Wyznacz równanie obrazu tego okręgu w jednokładności o środku \(S\) i skali \(k = −3\).
Dany jest trapez prostokątny \(A B C D\) o kątach prostych przy wierzchołkach \(A\) i \(D\). Ramię \(B C\) trapezu ma długość \(5\) . W ten trapez wpisano okrąg o środku w punkcie \(S\) i promieniu \(2\). Punkt \(P\) jest punktem styczności tego okręgu i dłuższej podstawy \(A B\) tego trapezu (zobacz rysunek). 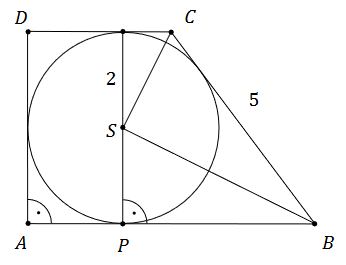
Wykaż, że trójkąty BPS i BSC są trójkątami podobnymi, oraz oblicz skalę tego podobieństwa. Zapisz obliczenia.

Punkt \(D\) leży wewnątrz trójkąta \(ABC\). Prosta przechodząca przez punkt \(D\) i równoległa do boku \(AC\) przecina bok \(AB\) w punkcie \(K\), a bok \(BC\) w punkcie \(L\). Prosta przechodząca przez punkt \(D\) i równoległa do boku \(BC\) przecina bok \(AB\) w punkcie \(M\), a bok \(AC\) w punkcie \(N\) (zobacz rysunek). Stosunek obwodu trójkąta \(KMD\) do obwodu trójkąta \(KBL\) jest równy \(5 : 7\), a stosunek obwodu trójkąta \(KMD\) do obwodu trójkąta \(AMN\) jest równy \(5 : 8\). Pole czworokąta \(DLCN\) jest równe \(15\). 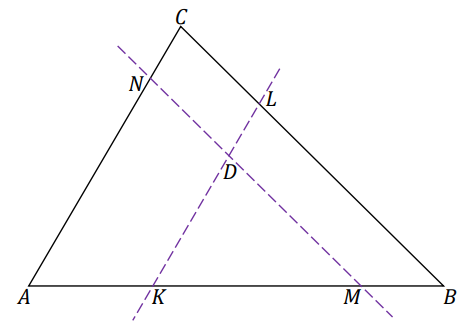

Oblicz pole trójkąta \(ABC\). Zapisz obliczenia.
Tematy nadrzędne