Matura rozszerzona - zbiór zadań - pierwiastki wielomianów

Drukuj

Poziom rozszerzony

Wyznacz pierwiastki całkowite wielomianu \( W(x)=x^4+2x^3-13x^2+4x-30 \).

Pierwiastków całkowitych wielomianu szukamy tylko wśród dzielników wyrazu wolnego \( -30 \).
Dzielnikami liczby \( -30 \) są: \[-1,\ 1,\ -2,\ 2,\ -3,\ 3,\ -5,\ 5,\ -6,\ 6,\ -10,\ 10,\ -15,\ 15,\ -30,\ 30\] Sprawdzamy wszystkie liczby po kolei:

\[\begin{split}W(-1)&={(-1)}^{4}+2\cdot {(-1)}^{3}-13\cdot {(-1)}^{2}+4\cdot (-1)-30=\\&=1-2-13-4-30=-48\ne 0\\\end{split}\] \[\begin{split}W(1)&={1}^{4}+2\cdot {1}^{3}-13\cdot {1}^{2}+4\cdot 1-30=\\&=1+2-13+4-30=-36\ne 0\\\end{split}\] \[\begin{split}W(-2)&={(-2)}^{4}+2\cdot {(-2)}^{3}-13\cdot {(-2)}^{2}+4\cdot (-2)-30=\\&=16-16-52-8-30=-90\ne 0\\\end{split}\] \[\begin{split}W(2)&={2}^{4}+2\cdot {2}^{3}-13\cdot {2}^{2}+4\cdot 2-30=\\&=16+16-52+8-30=-42\ne 0\\\end{split}\] \[\begin{split}W(-3)&={(-3)}^{4}+2\cdot {(-3)}^{3}-13\cdot {(-3)}^{2}+4\cdot (-3)-30=\\&=81-54-117-12-30=-132\ne 0\\\end{split}\] \[\begin{split}W(3)&={3}^{4}+2\cdot {3}^{3}-13\cdot {3}^{2}+4\cdot 3-30=\\&=81+54-117+12-30=0 \quad \Rightarrow \quad \text{3 jest pierwiastkiem}\end{split}\] \[\begin{split}W(-5)&={(-5)}^{4}+2\cdot {(-5)}^{3}-13\cdot {(-5)}^{2}+4\cdot (-5)-30=\\&=625-250-325-20-30=0 \quad \Rightarrow \quad -5 \text{ jest pierwiastkiem}\end{split}\] \[\begin{split}W(5)&={5}^{4}+2\cdot {5}^{3}-13\cdot {5}^{2}+4\cdot 5-30=\\&=625+250-325+20-30=540\ne 0\end{split}\]

Wartości wielomianu dla kolejnych dzielników przedstawię już bez wykonywania szczegółowych obliczeń:

\[W(-6)=366\ne 0\] \[W(6)=5326\ne 0\] \[W(-10)=6630\ne 0\] \[W(10)=10710\ne 0\] \[W(-15)=40860 \ne 0\] \[W(15)=54480\ne 0\] \[W(-30)=744150\ne 0\] \[W(30)=852390\ne 0\]

Odpowiedź: Całkowitymi pierwiastkami wielomianu \( W(x) \) są: \( x=3 \) oraz \( x=-5 \).

Uwaga! Zazwyczaj nie trzeba wykonywać szczegółowych obliczeń dla wszystkich dzielników. Dla wielu liczb od razu "na oko" widać, że wielomian dla nich się nie wyzeruje.
Ponadto zawsze warto zacząć sprawdzanie od najmniejszych dzielników.

Wyznacz pierwiastki wymierne wielomianu \( W(x)=3x^3-x^2+3x-1\).

Pierwiastków wymiernych wielomianu szukamy wśród liczb postaci \( \frac{p}{q} \), gdzie \( p \) jest dzielnikiem wyrazu wolnego (czyli liczby \( -1 \)), a \( q \) jest dzielnikiem współczynnika przy \( x^3 \) ( czyli liczby \( 3 \)).
Zatem liczba \( p \) może być równa: \[-1,\ 1\] a liczba \( q \) może być równa: \[-1,\ 1,\ -3,\ 3\] Zatem liczby \( \frac{p}{q} \), które mogą być pierwiastkami wymiernymi wielomianu, to:
\[-1,\ 1,\ -\frac{1}{3},\ \frac{1}{3}\] Sprawdzamy wszystkie liczby po kolei:

\[W(-1)=3\cdot {(-1)}^{3}-{(-1)}^{2}+3\cdot (-1)-1=-3-1-3-1=-8\ne 0\] \[W(1)=3\cdot {1}^{3}-{1}^{2}+3\cdot 1-1=3-1+3-1=4\ne 0\] \[W\left ( -\frac{1}{3} \right )=3\cdot {\left ( -\frac{1}{3} \right )}^{3}-{\left ( -\frac{1}{3} \right )}^{2}+3\cdot \left ( -\frac{1}{3} \right )-1=-\frac{1}{9}-\frac{1}{9}-1-1=-2\frac{2}{9}\ne 0\] \[W\left ( \frac{1}{3} \right )=3\cdot {\left ( \frac{1}{3} \right )}^{3}-{\left ( \frac{1}{3} \right )}^{2}+3\cdot \left ( \frac{1}{3} \right )-1=\frac{1}{9}-\frac{1}{9}+1-1= 0\]

Odpowiedź: Jedynym pierwiastkiem wymiernym wielomianu \( W(x) \) jest \( x=\frac{1}{3} \).
Uwaga!
Tego typu zadania można również rozwiązywać rozkładając wielomian na iloczyn czynników: \[W(x)=3x^3-x^2+3x-1 = x^2(3x-1)+(3x-1)=(3x-1)(x^2+1)\] Teraz z postaci iloczynowej od razu widać, że jedynym pierwiastkiem wielomianu jest \( x=\frac{1}{3} \).
Twierdzenie o wymiernych pierwiastkach wielomianu stosujemy wtedy, gdy nie jesteśmy w stanie rozłożyć wielomianu na iloczyn czynników.

Wielomian \( W(x)=x^4+bx^3+cx^2+dx+1 \), gdzie \(b, c, d\) są liczbami całkowitymi, ma dwa różne pierwiastki wymierne. Podaj te pierwiastki.

Pierwiastków wymiernych wielomianu szukamy wśród liczb postaci \( \frac{p}{q} \), gdzie \( p \) jest dzielnikiem wyrazu wolnego (czyli liczby \( 1 \)), a \( q \) jest dzielnikiem współczynnika przy \( x^4 \) ( czyli liczby \( 1 \)).
Zatem liczba \( p \) może być równa: \[-1,\ 1\] a liczba \( q \) może być równa: \[-1,\ 1\] Zatem liczby \( \frac{p}{q} \), które mogą być pierwiastkami wymiernymi wielomianu, to:
\[-1,\ 1\]

Z treści zadania wiemy, że wielomian \( W(x) \) ma dwa pierwiastki wymierne, zatem muszą to być właśnie te pierwiastki, czyli: \( x=-1 \) oraz \( x=1 \) (innych możliwości na pierwiastki wymierne nie ma).

Odpowiedź: Szukane pierwiastki wielomianu to: \( x=-1 \) oraz \( x=1 \).

Wielomian \( W(x)=2x^4+bx^3+cx^2+dx+5 \), gdzie \(b, c, d\) są liczbami całkowitymi, ma dwa różne pierwiastki, które są liczbami całkowitymi ujemnymi. Podaj te pierwiastki.

Pierwiastków całkowitych wielomianu szukamy tylko wśród dzielników wyrazu wolnego \( -5 \).
Dzielnikami liczby \( -5 \) są: \[-1,\ 1,\ -5,\ 5\]

Wiemy, że wielomian ma dwa różne pierwiastki, które są liczbami całkowitymi ujemnymi. Wśród powyższych liczb mamy tylko dwie liczby całkowite ujemne: \( -1,\ -5 \). Zatem to są właśnie szukane pierwiastki.

Odpowiedź: Szukane pierwiastki wielomianu to: \( x=-1 \) oraz \( x=-5 \).

Na rysunku przedstawiono fragment wykresu wielomianu \(W\) określonego wzorem \[ W(x)=\frac{1}{8} x^{3}-2 x^{2}+\frac{67}{8} x-3 \] dla każdego \(x \in \mathbb{R}\).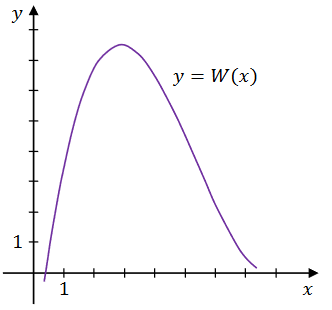

Oblicz wszystkie pierwiastki wielomianu \(W\). Zapisz obliczenia.

\(4-\sqrt{13}\), \(4+\sqrt{13}\) oraz \(8\)

Wielomian \(W\) jest określony wzorem \(W(x)=(x-1)\left(x^{2}-m x+m-1\right)\) dla każdego \(x \in \mathbb{R}\).

Wyznacz wszystkie wartości parametru \(\boldsymbol{m}\), dla których wielomian \(\boldsymbol{W}\) ma dokładnie jeden pierwiastek rzeczywisty. Zapisz obliczenia.

\(m=2\)