Matura rozszerzona - zbiór zadań - kombinatoryka
Poziom rozszerzony
W tym zbiorku umieściłem zadania z kombinatoryki oraz z klasycznego rachunku prawdopodobieństwa.Na okręgu zaznaczono sześć różnych punktów. Ile różnych wielokątów wypukłych o wszystkich wierzchołkach w tych punktach można narysować?
Oblicz, ile jest liczb naturalnych sześciocyfrowych, w zapisie których występuje dokładnie trzy razy cyfra \(0\) i dokładnie raz występuje cyfra \(5\).
Oblicz, ile jest trzycyfrowych liczb całkowitych dodatnich, w których zapisie dziesiętnym występują dokładnie dwie różne cyfry.
Rozpatrujemy wszystkie liczby naturalne dziesięciocyfrowe, w zapisie których mogą występować wyłącznie cyfry \(1\), \(2\), \(3\), przy czym cyfra \(1\) występuje dokładnie trzy razy. Uzasadnij, że takich liczb jest \(15360\).
Wśród \(n\) osób są Ania i jej dwaj znajomi. Wszystkie te \(n\) osób ustawiamy w kolejkę jedna za drugą. Liczba wszystkich takich ustawień jest \(12\) razy większa od liczby wszystkich takich ustawień tych \(n\) osób w kolejkę, w których Ania i jej dwaj znajomi zajmują trzy kolejne miejsca (w dowolnej kolejności).
Oblicz \(n\). Zapisz obliczenia.
Rozważamy wszystkie liczby naturalne pięciocyfrowe zapisane przy użyciu cyfr \(1\), \(3\), \(5\), \(7\), \(9\), bez powtarzania jakiejkolwiek cyfry. Oblicz sumę wszystkich takich liczb.
Oblicz, ile jest wszystkich siedmiocyfrowych liczb naturalnych, w których zapisie dziesiętnym występują dokładnie trzy cyfry \(1\) i dokładnie dwie cyfry \(2\).
Zbiór \(A=\{1,2,3,...,2n-1,2n\}\), gdzie \(n\ge 4\), jest złożony z \(2n\) kolejnych liczb naturalnych. Rozpatrujemy wszystkie czteroelementowe podzbiory zbioru \(A\). Przez \(x\) oznaczmy liczbę podzbiorów, których suma wszystkich elementów jest parzysta, a przez \(y\) oznaczmy liczbę podzbiorów, których suma wszystkich elementów jest nieparzysta. Wykaż, że \(x-y=\binom{n}{2} \).
Rzucamy cztery razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że iloczyn liczb oczek otrzymanych we wszystkich czterech rzutach będzie równy \(60\).
W zielonym pudełku jest 10 monet pięciozłotowych i 5 monet dwuzłotowych, a w białym pudełku są 2 monety pięciozłotowe i 3 monety dwuzłotowe. Z zielonego pudełka losujemy jedną monetę i wrzucamy ją do białego pudełka. Następnie z białego pudełka losujemy jednocześnie 2 monety. Oblicz prawdopodobieństwo, że z białego pudełka wylosujemy w sumie 7 złotych.
W pudełku znajduje się \(8\) piłeczek oznaczonych kolejnymi liczbami naturalnymi od \(1\) do \(8\). Losujemy jedną piłeczkę, zapisujemy liczbę na niej występującą, a następnie zwracamy piłeczkę do urny. Tę procedurę wykonujemy jeszcze dwa razy i tym samym otrzymujemy zapisane trzy liczby. Oblicz prawdopodobieństwo wylosowania takich piłeczek, że iloczyn trzech zapisanych liczb jest podzielny przez \(4\). Wynik podaj w postaci ułamka zwykłego.
W urnie I jest \(7\) czarnych kul, a w urnie II są \(3\) czarne kule. Do tych urn wkładamy losowo w sumie \(3\) kule białe. Następnie losujemy urnę i z urny jedną kulę. Oblicz, ile należy wrzucić białych kul do urny I, aby prawdopodobieństwo wylosowania białej kuli z losowo wybranej urny było równe \(\frac{17}{72}\).
Niech \(n\) będzie ustaloną liczbą naturalną dodatnią. Ze zbioru \(\mathbb{M}=\{1 ; 2 ; 3 ; \ldots ; 3 n+1\}\) losujemy jednocześnie trzy liczby. Zdarzenie \(A\) odpowiada jednoczesnemu wylosowaniu ze zbioru \(\mathbb{M}\) trzech liczb, których suma przy dzieleniu przez \(3\) daje resztę \(1\).
Oblicz prawdopodobieństwo zdarzenia \(\boldsymbol{A}\). Zapisz obliczenia.
Z liczb ośmioelementowego zbioru \(Z = \{1, 2, 3, 4, 5, 6, 7, 9\}\) tworzymy ośmiowyrazowy ciąg, którego wyrazy się nie powtarzają. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że żadne dwie liczby parzyste nie są sąsiednimi wyrazami utworzonego ciągu. Wynik przedstaw w postaci ułamka zwykłego nieskracalnego.
W urnie umieszczono \(4\) kule białe i \(8\) kul czarnych. Losujemy jedną kulę. Jeżeli będzie biała, to wrzucamy ją z powrotem do urny i dorzucamy do niej jeszcze dwie białe kule. Jeżeli będzie czarna, to zatrzymujemy ją i dorzucamy dwie zielone kule do urny. Następnie losujemy z urny jednocześnie dwie kule. Oblicz prawdopodobieństwo zdarzenia, że obie z wylosowanych za drugim razem kul są białe.
W pewnym mieście jest prostopadły układ ulic, a ruch na każdej z nich jest dwukierunkowy. W centrum miasta znajduje się park, gdzie obowiązuje całkowity zakaz ruchu pojazdów. Schemat ulic w tym mieście wraz z położeniem parku przedstawiono poniżej na rysunku. Tomek znajduje się w punkcie \(A\) miasta i chce dojechać samochodem najkrótszą drogą do punktu \(B\). 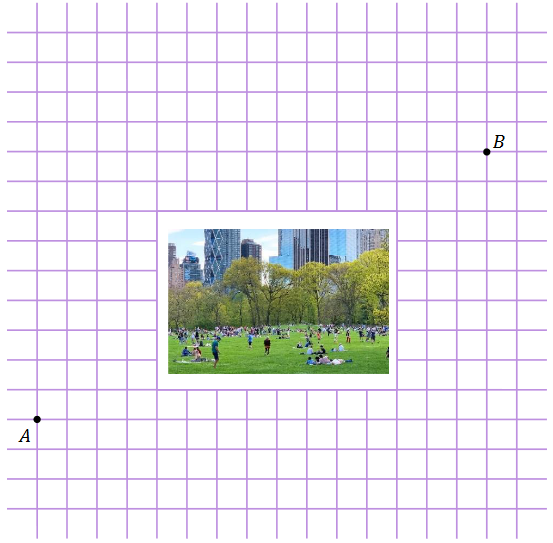
Oblicz, ile jest najkrótszych dróg z \(A\) do \(B\). Zapisz obliczenia.

Tematy nadrzędne