Matura rozszerzona - zbiór zadań - bryły obrotowe

Drukuj

Poziom rozszerzony

Iloczyn długości średnicy podstawy walca i wysokości walca jest równy \(12 \sqrt{3}\).
Pole powierzchni całkowitej tego walca jest równe \(12 \pi(\sqrt{3}+1)\).

Oblicz objętość tego walca. Zapisz obliczenia.

\(V=18\pi \sqrt{2}\)

Objętość stożka ściętego (przedstawionego na rysunku) można obliczyć ze wzoru \(V = \frac{1}{3} \pi H (r^2 + rR + R^2)\), gdzie \(r\) i \(R\) są promieniami podstaw (\(r \lt R\)), a \(H\) jest wysokością bryły. Dany jest stożek ścięty, którego wysokość jest równa \(10\), objętość \(840\pi\), a \(r = 6\). Oblicz cosinus kąta nachylenia przekątnej przekroju osiowego tej bryły do jednej z jej podstaw.

\(\cos \alpha = \frac{9\sqrt{106}}{106}\)

Tomek i Marek chcą wejść docelowo na szczyt \(S\) pewnej góry. W chwili początkowej znajdują się w punkcie \(P\) położonym na stoku góry dokładnie na północ od szczytu na wysokości \(H_{0}\) metrów n.p.m. Tomek i Marek chcą dotrzeć do bazy \(B\) znajdującej się dokładnie w połowie drogi na szczyt na południe od szczytu na przeciwległym południowym stoku góry na wysokości \(H_{1}\) metrów n.p.m., a następnie z bazy wejść na szczyt leżący na wysokości \(H_{2}\) metrów n.p.m. (zobacz rysunek 1.).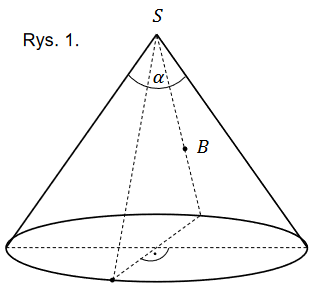

Oblicz długość najkrótszej drogi, jaką muszą pokonać, aby dotrzeć do bazy. Zapisz obliczenia.

Przyjmij, że góra jest stożkiem o kącie rozwarcia \(\alpha\).

Wskazówka: Powierzchnia boczna stożka po rozcięciu wzdłuż tworzącej i rozłożeniu jest wycinkiem koła. Najkrótsza droga do bazy odpowiada najkrótszej drodze z punktu \(P\) do \(B\) na wycinku koła.

\(d=\frac{\sqrt{\left(H_{2}-H_{0}\right)^{2}+\left(H_{2}-H_{1}\right)^{2}-2\left(H_{2}-H_{0}\right)\left(H_{2}-H_{1}\right) \cos \left(\pi \cdot \sin \frac{\alpha}{2}\right)}}{\cos \frac{\alpha}{2}}\)