Zbiór zadań - wzór funkcji kwadratowej
Poziom podstawowy
Wykresem funkcji kwadratowej \(f(x)=3x^2+bx+c\) jest parabola o wierzchołku w punkcie \(W=(-3,2)\). Wzór tej funkcji w postaci kanonicznej to
A.\( f(x)=3(x-3)^2+2 \)
B.\( f(x)=3(x+3)^2+2 \)
C.\( f(x)=(x-3)^2+2 \)
D.\( f(x)=(x+3)^2+2 \)
Dana jest funkcja \(f\) określona wzorem \(f(x)=x^2-b-2 \sqrt{2}\) dla każdej liczby rzeczywistej \(x\). Miejscem zerowym funkcji \(f\) jest \(x=\sqrt{2}+1\).
Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych.
Współczynnik \(b\) we wzorze funkcji \(f\) jest równy A.\((-3)\)
B.\(3\)
C.\(3-\sqrt{2}\)
D.\(3-2 \sqrt{2}\)
Zbiorem wartości funkcji kwadratowej \(f(x)=-\frac{1}{3}x^2-2x+c\) jest przedział \((-\infty ,7\rangle \). Zatem współczynnik \(c\) jest równy
A.\( -3 \)
B.\( 4 \)
C.\( 7 \)
D.\( 10 \)
W układzie współrzędnych narysowano część paraboli o wierzchołku w punkcie \( A=(2, 4) \), która jest wykresem funkcji kwadratowej \( f \). 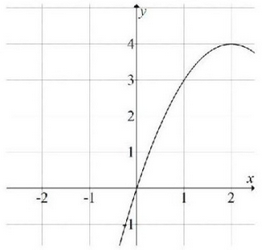 Funkcja \( f \) może być opisana wzorem
Funkcja \( f \) może być opisana wzorem
 Funkcja \( f \) może być opisana wzorem
Funkcja \( f \) może być opisana wzorem A.\(f(x)=(x-2)^2+4 \)
B.\(f(x)=(x+2)^2+4 \)
C.\(f(x)=-(x-2)^2+4 \)
D.\(f(x)=-(x+2)^2+4 \)
Dana jest funkcja kwadratowa \(f\), której fragment wykresu przedstawiono w kartezjańskim układzie współrzędnych \((x,y)\) na rysunku poniżej. Wierzchołek paraboli, która jest wykresem funkcji \(f\), oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite. 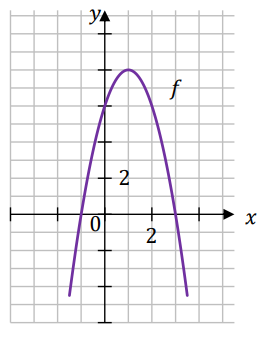

Funkcja \(g\) jest określona za pomocą funkcji \(f\) następująco: \(g(x)=f(x-2)\). 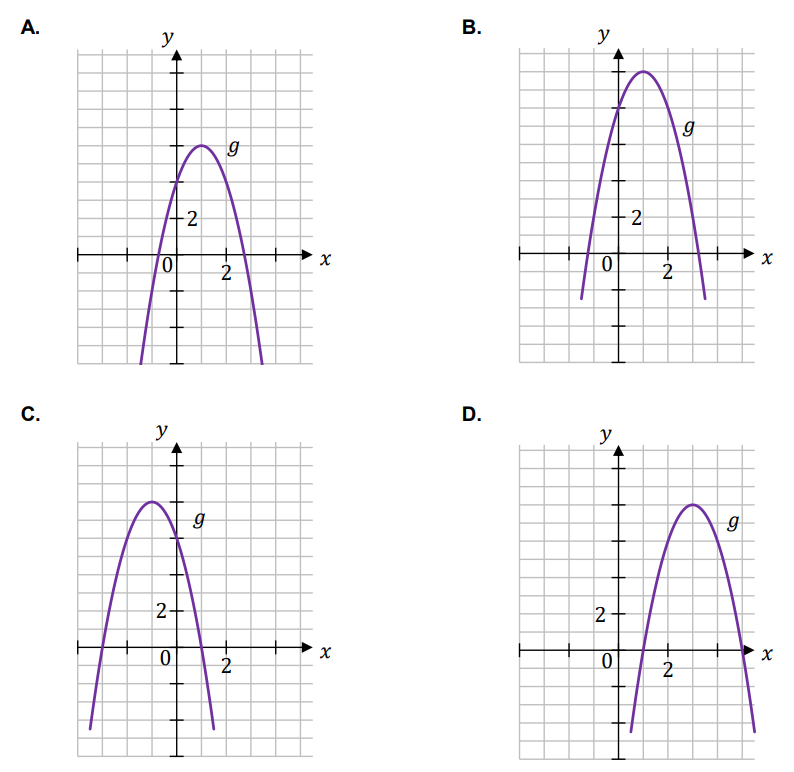
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Wykres funkcji \(g\) przedstawiono na rysunku 
Wyznacz i zapisz w miejscu wykropkowanym poniżej zbiór wszystkich rozwiązań nierówności: \[f(x)\le 0\] 

Wyznacz wzór funkcji kwadratowej \(f\) w postaci kanonicznej.
Zapisz obliczenia.
Zapisz obliczenia.
Wzór funkcji kwadratowej można zapisać w postaci ogólnej, kanonicznej lub iloczynowej (o ile istnieje).
Dana jest funkcja kwadratowa \(y=f(x)\), której fragment wykresu przedstawiono w kartezjańskim układzie współrzędnych \((x,y)\) na rysunku poniżej. 

Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych, jeżeli wiadomo, że jeden ze wzorów podanych w odpowiedziach A–D to wzór funkcji \(f\).
Funkcja kwadratowa \(y=f(x)\) jest określona wzorem A.\( y=-(x+5)^2-6 \)
B.\( y=-(x+5)^2+6 \)
C.\( y=-(x-5)^2-6 \)
D.\( y=-(x-5)^2+6 \)
Funkcja kwadratowa \(f\) określona wzorem \(f(x) = x^2 + bx + c\) osiąga dla \(x = 2\) wartość najmniejszą równą \(4\). Wtedy
A.\( b=-4,\ c=8 \)
B.\( b=4,\ c=-8 \)
C.\( b=-4,\ c=-8 \)
D.\( b=4,\ c=8 \)
Funkcja kwadratowa \(f\) określona wzorem \(f(x) = −2(x + 1)(x − 3)\) jest malejąca w przedziale
A.\( \langle 1,+\infty ) \)
B.\( (-\infty ,1\rangle \)
C.\( (-\infty ,-8\rangle \)
D.\( \langle -8,+\infty ) \)
Dana jest funkcja kwadratowa \(f\) określona wzorem \(f(x) = -2(x - 2)(x + 1)\). Funkcja \(f\) jest rosnąca w zbiorze
A.\( \left(-\infty, \frac{1}{2}\right\rangle \)
B.\( (-1,2) \)
C.\( \left(0, \frac{5}{2}\right) \)
D.\( \left\langle \frac{5}{2}, +\infty \right\rangle \)
Wykresem funkcji kwadratowej \( f(x)=2x^2+bx+c \) jest parabola, której wierzchołkiem jest punkt \( W=(4,0) \). Oblicz wartości współczynników \( b \) i \( c \).
Funkcja kwadratowa \(f\) określona jest wzorem \(f(x) = ax^2 + bx + c\). Zbiorem rozwiązań nierówności \(f(x) \gt 0\) jest przedział \((0,12)\). Największa wartość funkcji \(f\) jest równa \(9\). Oblicz współczynniki \(a\), \(b\) i \(c\) funkcji \(f\).
Wyznacz wzór funkcji kwadratowej \(f\) w postaci ogólnej, wiedząc, że zbiorem wartości tej funkcji jest przedział \((-\infty ,-1\rangle \), a wartość \(-5\) osiąga ona dla dwóch argumentów: \(2\) i \(10\).
Na rysunku są przedstawione fragmenty wykresów funkcji kwadratowych \(f\) i \(g\). Funkcja \(f\) jest określona wzorem \(f(x)=-x^2+6x-5\), a mniejsze z jej miejsc zerowych jest jednocześnie miejscem zerowym funkcji \(g\). Wierzchołek \(W\) paraboli, która jest wykresem funkcji \(f\), leży na wykresie funkcji \(g\), a wierzchołek \(Z\) paraboli będącej wykresem funkcji \(g\) leży na osi \(Oy\) układu współrzędnych. Wyznacz wzór funkcji \(g\). 

Funkcja kwadratowa \(f\) jest określona wzorem \(f(x)=3 x^{2}+2 x+m\) dla każdej liczby rzeczywistej \(x\). Współczynnik \(m\) jest liczbą rzeczywistą mniejszą od zera. 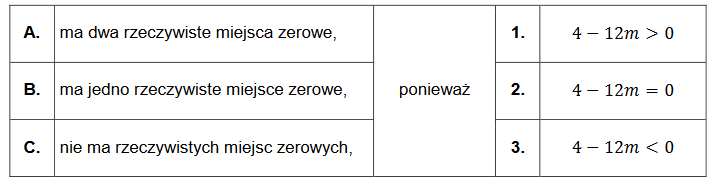
Dokończ zdanie. Zaznacz odpowiedź A, B albo C oraz jej uzasadnienie 1., 2. albo 3.
Funkcja \(f\) 
Tematy nadrzędne