Zbiór zadań - wykres funkcji kwadratowej
Poziom podstawowy
Dana jest funkcja kwadratowa \(y=f(x)\), której fragment wykresu przedstawiono w kartezjańskim układzie współrzędnych \((x,y)\) na rysunku poniżej. 
Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych, jeżeli wiadomo, że jeden ze wzorów podanych w odpowiedziach A–D to wzór funkcji \(f\).
Funkcja kwadratowa \(y=f(x)\) jest określona wzorem A.\( y=-(x+5)^2-6 \)
B.\( y=-(x+5)^2+6 \)
C.\( y=-(x-5)^2-6 \)
D.\( y=-(x-5)^2+6 \)
Funkcja kwadratowa \(f\) jest określona wzorem \(f(x)=-2(x+3)(x-5)\). Wierzchołek paraboli, która jest wykresem funkcji \(f\), ma współrzędną \(x\) równą
A.\( (-3) \)
B.\( (-1) \)
C.\( 1 \)
D.\( 5 \)
Funkcja \(f\) jest określona wzorem \(f(x)=-x^2+4\) dla każdej liczby rzeczywistej \(x\). Zbiorem wartości funkcji \(f\) jest przedział
A.\( (-\infty, -2\rangle \)
B.\( \langle 2, +\infty) \)
C.\( \langle -4, +\infty) \)
D.\( (-\infty, 4\rangle \)
Na rysunku przedstawiony jest fragment paraboli będącej wykresem funkcji kwadratowej \(f\). Wierzchołkiem tej paraboli jest punkt \(W = (2, -4)\). Liczby \(0\) i \(4\) to miejsca zerowe funkcji \(f\). 
Zbiorem wartości funkcji \(f\) jest przedział
Zbiorem wartości funkcji \(f\) jest przedział A.\( (-\infty , 0\rangle \)
B.\( \langle 0, 4\rangle \)
C.\( \langle -4, +\infty) \)
D.\( \langle 4, +\infty) \)
Na rysunku przedstawiono fragment wykresu funkcji kwadratowej \(f\). 
Jeden spośród podanych poniżej wzorów jest wzorem tej funkcji. Wskaż wzór funkcji \(f\).
Jeden spośród podanych poniżej wzorów jest wzorem tej funkcji. Wskaż wzór funkcji \(f\). A.\( f(x)=x^2-6x+11 \)
B.\( f(x)=-x^2+x+2 \)
C.\( f(x)=x^2-6x-7 \)
D.\( f(x)=-x^2+6x-7 \)
Na jednym z rysunków przedstawiono fragment wykresu funkcji kwadratowej określonej wzorem \(f(x)=-(x-1)(3-x)\). Wskaż ten rysunek.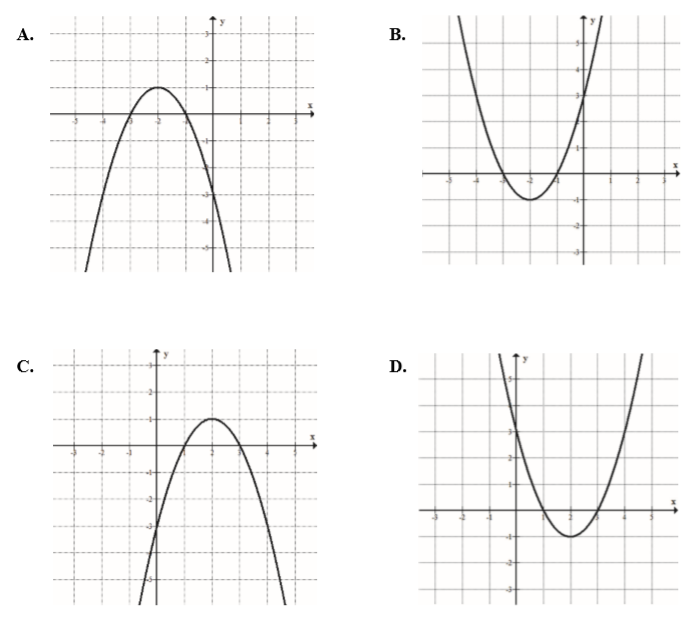 
Zbiorem wartości funkcji \(f(x)=-(x+7)(x-3)\) jest:
A.\( (-\infty ;25\rangle \)
B.\( (-\infty ;-2\rangle \)
C.\( \langle 25;+\infty ) \)
D.\( (-\infty ;2\frac{1}{2}\rangle \)
Osią symetrii wykresu funkcji \(f\) jest prosta o równaniu
A.\( y = -4 \)
B.\( x = -4 \)
C.\( y = 2 \)
D.\( x = 2 \)
Na rysunku przedstawiono fragment paraboli będącej wykresem funkcji kwadratowej \(g\). Wierzchołkiem tej paraboli jest punkt \(W=(1,1)\). 
Zbiorem wartości funkcji \(g\) jest przedział
Zbiorem wartości funkcji \(g\) jest przedział A.\( (-\infty ,0\rangle \)
B.\( \langle ,2 \rangle \)
C.\( \langle 1,+\infty ) \)
D.\( (-\infty ,1\rangle \)
Do wykresu pewnej funkcji kwadratowej \(y=g(x)\) należy punkt o współrzędnych \(P=(2,-6)\). Osią symetrii wykresu tej funkcji jest prosta o równaniu \(x=3\), a jednym z miejsc zerowych funkcji \(g\) jest \(x_1=1\).
Wyznacz i zapisz wzór funkcji \(y=g(x)\) w postaci iloczynowej.
W kartezjańskim układzie współrzędnych \((x, y)\) wykresem funkcji kwadratowej \(f\) jest parabola, której wierzchołkiem jest punkt \((3,0)\). Ta parabola przechodzi przez punkt o współrzędnych \((0,-9)\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Funkcja \(f\) jest malejąca w przedziale A.\((-\infty, 0]\)
B.\((-\infty, 3]\)
C.\([0,+\infty)\)
D.\([3,+\infty)\)
Uzupełnij zdanie. Wybierz dwie właściwe odpowiedzi spośród oznaczonych literami A-F i wpisz te litery w wykropkowanych miejscach.
Wzór funkcji \(f\) zapisano w odpowiedziach oznaczonych literami: .......... oraz .......... . A.\(f(x)=-x^{2}-9\)
B.\(f(x)=-(x-3)^{2}\)
C.\(f(x)=-(x+3)^{2}\)
D.\(f(x)=-x^{2}+6 x-9\)
E.\(f(x)=-x^{2}-6 x+9\)
F.\(f(x)=-x^{2}-6 x-9\)
Funkcja kwadratowa \(g\) jest określona za pomocą funkcji \(f\) następująco: \(g(x)=f(x)-1\).
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
| Funkcja \(g\) ma jedno miejsce zerowe. | P | F |
| W kartezjańskim układzie współrzędnych \((x, y)\) osią symetrii wykresu funkcji \(g\) jest prosta o równaniu \(x=3\). | P | F |
Tematy nadrzędne