Zbiór zadań - układy równań liniowych

Drukuj

Poziom podstawowy

Rozwiązaniem układu równań \begin{cases} 11x-11y=1 \\ 22x+22y=-1 \end{cases} jest para liczb: \(x=x_0\), \(y=y_0\). Wtedy

A.\( x_0\gt 0 \) i \(y_0 \gt 0\)

B.\( x_0\gt 0 \) i \(y_0 \lt 0\)

C.\( x_0\lt 0 \) i \(y_0 \gt 0\)

D.\( x_0\lt 0 \) i \(y_0 \lt 0\)

Para liczb \(x = 2\) i \(y = 2\) jest rozwiązaniem układu równań \(\begin{cases} ax + y = 4 \\ -2x + 3y = 2a \end{cases}\) dla

A.\( a = -1 \)

B.\( a = 1 \)

C.\( a = -2 \)

D.\( a = 2 \)

\(a = 1\)

Układ równań \(\begin{cases} 2x-y=2 \\ x+my=1 \end{cases} \) ma nieskończenie wiele rozwiązań dla

A.\( m=-1 \)

B.\( m=1 \)

C.\( m=\frac{1}{2} \)

D.\( m=-\frac{1}{2} \)

Para liczb \(x=3\) i \(y=1\) jest rozwiązaniem układu równań \(\begin{cases} -x+12y=a^2 \\ 2x+ay=9 \end{cases} \) dla

A.\( a=\frac{7}{3} \)

B.\( a=-3 \)

C.\( a=3 \)

D.\( a=-\frac{7}{3} \)

Para liczb \(x = 1\), \(y = −3\) spełnia układ równań \begin{cases} x-y=a^2 \\ (1+a)x-3y=-4a \end{cases} Wtedy \(a\) jest równe

A.\( 2 \)

B.\( -2 \)

C.\( \sqrt{2} \)

D.\( -\sqrt{2} \)

Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych.

Układ równań \(\left\{\begin{array}{c}x+2 y=1 \\ -4 x-8 y=-4\end{array}\right.\)

A.nie ma rozwiązań.

B.ma dokładnie jedno rozwiązanie.

C.ma dokładnie dwa rozwiązania.

D.ma nieskończenie wiele rozwiązań.

Para liczb \(x=-1\) i \(y=6\) jest rozwiązaniem układu równań \[ \left\{\begin{array}{l} a x+3 y=20 \\ x+b y=5 \end{array}\right. \] gdzie \(a\) oraz \(b\) są liczbami rzeczywistymi.

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Wartość wyrażenia \(a \cdot b\) jest równa

A.\((-2)\)

B.\((-0,5)\)

C.\(0,5\)

D.\(2\)

Dane są dwie przecinające się proste. Miary kątów utworzonych przez te proste zapisano za pomocą wyrażeń algebraicznych (zobacz rysunek).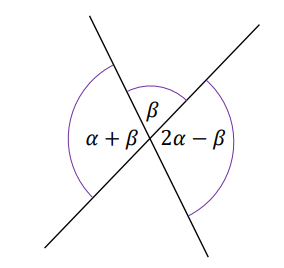

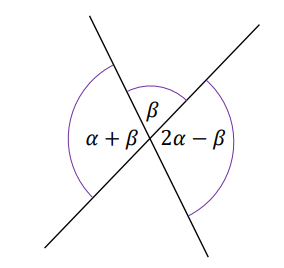
Dokończ zdanie. Wybierz dwie odpowiedzi, tak aby dla każdej z nich dokończenie poniższego zdania było prawdziwe.

Układem równań, w którym zapisano prawidłowe zależności między miarami kątów utworzonych przez te proste, jest układ

A.\( \begin{cases} (\alpha +\beta )+\beta =90^\circ \\ \alpha +\beta =2\alpha -\beta \end{cases} \)

B.\( \begin{cases} (\alpha +\beta )+\beta =180^\circ \\ \alpha +\beta =2\alpha -\beta \end{cases} \)

C.\( \begin{cases} (\alpha +\beta )+\beta =180^\circ \\ \beta =2\alpha -\beta \end{cases} \)

D.\( \begin{cases} \alpha +\beta =90^\circ \\ \beta =2\alpha -\beta \end{cases} \)

E.\( \begin{cases} \alpha +\beta =2\alpha -\beta \\ 180^\circ -(2\alpha -\beta )=\beta \end{cases} \)

F.\( \begin{cases} 3\alpha +2\beta =360^\circ \\ 2\alpha -\beta =2\beta \end{cases} \)