Zbiór zadań - twierdzenie cosinusów i wzór na pole trójkąta
Poziom podstawowy
Pole trójkąta o bokach długości \(4\) oraz \(9\) i kącie między nimi o mierze \(60^\circ\) jest równe
A.\( 18 \)
B.\( 9 \)
C.\( 18\sqrt{3} \)
D.\( 9\sqrt{3} \)
Pole trójkąta przedstawionego na rysunku wynosi 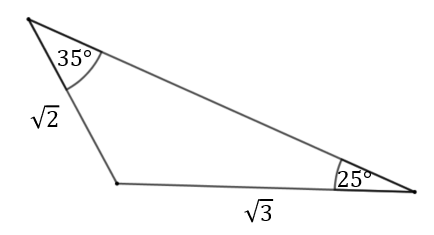

A.\( \frac{3}{4}\sqrt{2} \)
B.\( \sqrt{6} \)
C.\( \frac{\sqrt{6}}{2} \)
D.\( \frac{\sqrt{6}}{4} \)
Każde z ramion trójkąta równoramiennego ma długość \(20\). Kąt zawarty między ramionami tego trójkąta ma miarę \(150^\circ \). Pole tego trójkąta jest równe
A.\( 100 \)
B.\( 200 \)
C.\( 100\sqrt{3} \)
D.\( 100\sqrt{2} \)
Dany jest trójkąt \(ABC\), w którym \(|AB| = 6\), \(|BC| = 5\), \(|AC| = 10\).
Oceń prawdziwość poniższych stwierdzeń. Wybierz P, jeśli stwierdzenie jest prawdziwe, albo F – jeśli jest fałszywe.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe. | Cosinus kąta \(ABC\) jest równy \((−0{,}65)\). | P | F |
| Trójkąt \(ABC\) jest rozwartokątny. | P | F |
W trójkącie \(ABC\) dane są długości dwóch boków \(|AB| = 12\), \(|BC| = 8\) oraz miara kąta \(|\sphericalangle ABC| = 60^\circ\).
Oblicz długość środkowej tego trójkąta, poprowadzonej z wierzchołka \(A\).
Wierzchołki \(A\) i \(C\) trójkąta \(ABC\) leżą na okręgu o promieniu \(r\). Środek \(S\) tego okręgu leży na boku \(AB\) tego trójkąta (zobacz rysunek poniżej). Długości boków \(AB\) i \(AC\) są równe odpowiednio \(|AB| = 3r\) oraz \(|AC| = \sqrt{3}r\). 

Oblicz miary wszystkich kątów wewnętrznych trójkąta \(ABC\).
Dany jest trójkąt równoramienny, w którym ramię o długości \( 20 \) tworzy z podstawą kąt \( 67{,}5^\circ \). Pole tego trójkąta jest równe
A.\( 100\sqrt{3} \)
B.\( 100\sqrt{2} \)
C.\( 200\sqrt{3} \)
D.\( 200\sqrt{2} \)
Dany jest trójkąt \(ABC\) o bokach długości \(4\) i \(6\) . Pole tego trójkąta jest równe \(3\sqrt{15}\). Oznacza to, że jeśli kąt między bokami o długościach \(4\) i \(6\) ma miarę \(\alpha \gt 90^\circ \), to:
A.\( \cos \alpha =\frac{\sqrt{15}}{4} \)
B.\( \cos \alpha =\frac{1}{4} \)
C.\( \cos \alpha =-\frac{\sqrt{15}}{4} \)
D.\( \cos \alpha =-\frac{1}{4} \)
Tematy nadrzędne