Zbiór zadań - trójkąty
Poziom podstawowy
Wysokość trójkąta równobocznego jest równa \(6\sqrt{3}\). Pole tego trójkąta jest równe
A.\( 3\sqrt{3} \)
B.\( 4\sqrt{3} \)
C.\( 27\sqrt{3} \)
D.\( 36\sqrt{3} \)
Pole pewnego trójkąta równobocznego jest równe \(\frac{4\sqrt{3}}{9}\). Obwód tego trójkąta jest równy
A.\( 4 \)
B.\( 2 \)
C.\( \frac{4}{3} \)
D.\( \frac{2}{3} \)
Dany jest trójkąt równoboczny \(ABC\) o boku długości \(10\) cm. W tym trójkącie poprowadzono wysokość \(CD\). Obwód trójkąta \(ADC\) jest równy
A.\( 10\sqrt{3}\) cm
B.\( 20\sqrt{3} \) cm
C.\( (5+5\sqrt{3})\) cm
D.\( 15+5\sqrt{3})\) cm
Trójkąt \(ABC\) jest równoboczny. Punkt \(E\) leży na wysokości \(CD\) tego trójkąta oraz \(|CE|=\frac{3}{4}|CD|\). Punkt \(F\) leży na boku \(BC\) i odcinek \(EF\) jest prostopadły do \(BC\) (zobacz rysunek).  Wykaż, że \(|CF|=\frac{9}{16}|CB|\)
Wykaż, że \(|CF|=\frac{9}{16}|CB|\)
 Wykaż, że \(|CF|=\frac{9}{16}|CB|\)
Wykaż, że \(|CF|=\frac{9}{16}|CB|\)Trójkąt równoboczny \(ABC\) ma pole równe \(9\sqrt{3}\). Prosta równoległa do boku \(BC\) przecina boki \(AB\) i \(AC\) - odpowiednio - w punktach \(K\) i \(L\). Trójkąty \(ABC\) i \(AKL\) są podobne, a stosunek długości boków tych trójkątów jest równy \(\frac{2}{3}\). Oblicz długość boku trójkąta \(AKL\).
Kąt ostry rombu ma miarę \(60^\circ \), a bok tego rombu ma długość równą \(4\) cm.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe. | Krótsza przekątna dzieli ten romb na dwa trójkąty równoboczne. | P | F |
| Pole tego rombu jest równe \(8\sqrt{3}\ \text{cm}^2\). | P | F |
Najdłuższa przekątna sześciokąta foremnego ma długość \(8\). Wówczas pole koła opisanego na tym sześciokącie jest równe
A.\( 4\pi \)
B.\( 8\pi \)
C.\( 16\pi \)
D.\( 64\pi \)
Dłuższa przekątna sześciokąta foremnego ma długość \(2\sqrt{2}\). Pole tego sześciokąta jest równe
A.\( 12\sqrt{3} \)
B.\( 6\sqrt{3} \)
C.\( 2\sqrt{3} \)
D.\( 3\sqrt{3} \)
Z odcinków o długościach: \(5, 2a+1, a-1\) można zbudować trójkąt równoramienny. Wynika stąd, że
A.\( a=6 \)
B.\( a=4 \)
C.\( a=3 \)
D.\( a=2 \)
Dany jest trójkąt równoramienny \(ABC\), w którym \(|AC|=|BC|\). Na podstawie \(AB\) tego trójkąta leży punkt \(D\), taki że \(|AD|=|CD|\), \(|BC|=|BD|\) oraz \(\sphericalangle BCD=72^\circ \) (zobacz rysunek).  Wynika stąd, że kąt \(ACD\) ma miarę
Wynika stąd, że kąt \(ACD\) ma miarę
 Wynika stąd, że kąt \(ACD\) ma miarę
Wynika stąd, że kąt \(ACD\) ma miarę A.\( 38^\circ \)
B.\( 36^\circ \)
C.\( 42^\circ \)
D.\( 40^\circ \)
W trójkącie \(ABC\) kąt przy wierzchołku \(A\) jest prosty, a kąt przy wierzchołku \(B\) ma miarę \(30^\circ \). Na boku \(AB\) tego trójkąta obrano punkt \(D\) tak, że miara kąta \(CDA\) jest równa \(60^\circ \) oraz \(|AD|=6\) (zobacz rysunek). Oblicz \(|BD|\). 

Dany jest trójkąt prostokątny, którego przyprostokątne mają długości \(a\) i \(b\). Punkt \(O\) leży na przeciwprostokątnej tego trójkąta i jest środkiem okręgu stycznego do przyprostokątnych tego trójkąta (zobacz rysunek). 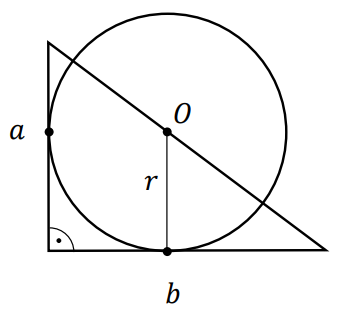 Wykaż, że promień \(r\) tego okręgu jest równy \(\frac{ab}{a+b}\)
Wykaż, że promień \(r\) tego okręgu jest równy \(\frac{ab}{a+b}\)
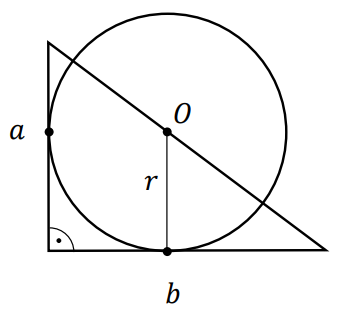 Wykaż, że promień \(r\) tego okręgu jest równy \(\frac{ab}{a+b}\)
Wykaż, że promień \(r\) tego okręgu jest równy \(\frac{ab}{a+b}\)Dany jest trójkąt \(ABC\). Punkt \(S\) jest środkiem boku \(AB\) tego trójkąta (zobacz rysunek). Wykaż, że odległości punktów \(A\) i \(B\) od prostej \(CS\) są równe. 

Dany jest trójkąt rozwartokątny \(ABC\), w którym \(\sphericalangle ACB\) ma miarę \(120^\circ \). Ponadto wiadomo, że \(|BC|=10\) i \(|AB|=10\sqrt{7}\) (zobacz rysunek). Oblicz długość trzeciego boku trójkąta \(ABC\). 

W trójkącie prostokątnym \(ACB\) przyprostokątna \(AC\) ma długość \(5\), a promień okręgu wpisanego w ten trójkąt jest równy \(2\). Oblicz pole trójkąta \(ACB\).
Dany jest trójkąt prostokątny \(ABC\). Promień okręgu wpisanego w ten trójkąt jest pięć razy krótszy od przeciwprostokątnej tego trójkąta. Oblicz sinus tego z kątów ostrych trójkąta \(ABC\), który ma większą miarę.
Trójkąt ostrokątny \(ABC\) jest wpisany w okrąg o środku \(O\) i promieniu \(4\). Kąt \(CAB\) jest równy kątowi \(OCB\) oraz kąt \(CBA\) jest równy kątowi \(OCA\). Oblicz długość wysokości \(CD\) opuszczonej z wierzchołka \(C\) na bok \(AB\).
Punkt \(S\) jest środkiem ciężkości trójkąta \(ABC\). Długość odcinka \(SA\) jest równa \(10\).
Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych.
Długość środkowej poprowadzonej z wierzchołka \(A\) do boku \(B C\) jest równa A.\( 10 \)
B.\( 15 \)
C.\( 20 \)
D.\( 30 \)
Dany jest trójkąt prostokątny \(A B C\) o bokach \(|A C|=12,|B C|=5,|A B|=13\). Dwusieczne kątów tego trójkąta przecinają się w punkcie \(P\) (zobacz rysunek). 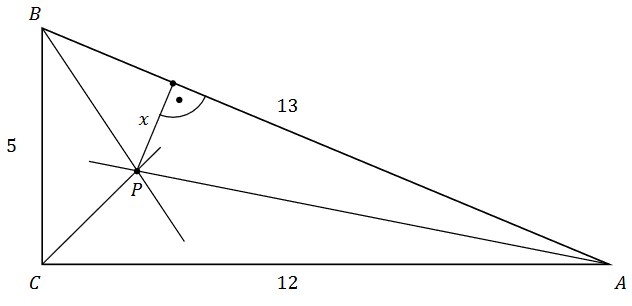

Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych.
Odległość \(x\) punktu \(P\) od przeciwprostokątnej \(AB\) jest równa A.\( 1 \)
B.\( 2 \)
C.\( \frac{5}{2} \)
D.\( \frac{20}{13} \)
Tematy nadrzędne