Zbiór zadań - statystyka
Poziom podstawowy
Średnia arytmetyczna dziesięciu liczb naturalnych \(3, 10, 5, x, x, x, x, 12, 19, 7\) jest równa \(12\). Mediana tych liczb jest równa
A.\( 14 \)
B.\( 12 \)
C.\( 16 \)
D.\( x \)
Średnia arytmetyczna zestawu sześciu liczb: \(2x,\ 4,\ 6,\ 8,\ 11,\ 13\) jest równa \(5\). Wynika stąd, że
A.\( x=-1 \)
B.\( x=7 \)
C.\( x=-6 \)
D.\( x=6 \)
Do szkolnego koła czytelniczego należy \(50\) uczniów. Opiekun koła zebrał dane dotyczące liczby książek przeczytanych przez tych uczniów w listopadzie 2024 roku. W poniższej tabeli przedstawiono wyniki zebrane przez opiekuna. 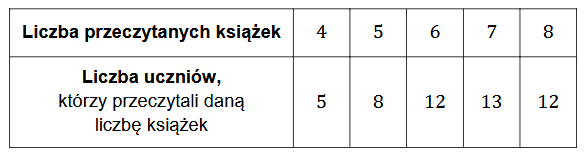
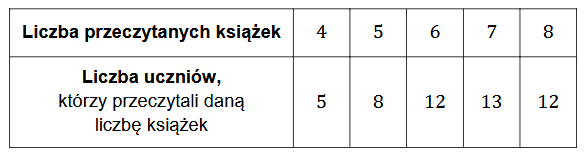
Uzupełnij zdania. Wpisz odpowiednie liczby w wykropkowanych miejscach, aby zdania były prawdziwe.
- Średnia arytmetyczna liczby przeczytanych książek w tej grupie uczniów jest równa ............ .
- Mediana liczby przeczytanych książek w tej grupie uczniów jest równa ............ .
Wyniki sprawdzianu z matematyki są przedstawione na poniższym diagramie.  Średnia ocen uzyskanych przez uczniów z tego sprawdzianu jest równa
Średnia ocen uzyskanych przez uczniów z tego sprawdzianu jest równa
 Średnia ocen uzyskanych przez uczniów z tego sprawdzianu jest równa
Średnia ocen uzyskanych przez uczniów z tego sprawdzianu jest równa A.\( 2 \)
B.\( 3 \)
C.\( 3{,}5 \)
D.\( 4 \)
Średnia arytmetyczna wszystkich liczb pierwszych z przedziału \( \langle 1; 13 ) \) jest równa:
A.\(5{,}6 \)
B.\(\frac{29}{6} \)
C.\(\frac{41}{6} \)
D.\(6 \)
Na wykresie słupkowym poniżej podano rozkład miesięcznych zarobków wszystkich pracowników w pewnej firmie \(F\). Na osi poziomej podano - wyrażone w tysiącach złotych - miesięczne wynagrodzenie netto pracowników firmy \(F\), a na osi pionowej przedstawiono liczbę osób, która osiąga podane zarobki. 

Dokończ zdanie. Zaznacz odpowiedź A, B albo C oraz jej uzasadnienie 1., 2. albo 3.
Dominantą miesięcznych zarobków w firmie \(F\) jest 
Uzupełnij zdanie. Wpisz odpowiednią liczbę w wykropkowanym miejscu, aby zdanie było prawdziwe.
Medianą miesięcznych zarobków w firmie \(F\) jest ................. tys. zł.Oblicz, jaki \(\%\) liczby wszystkich pracowników firmy \(F\) stanowią osoby zarabiające \(5{,}5\) tys. zł lub mniej.
Oblicz średnią miesięcznego wynagrodzenia netto wszystkich pracowników firmy \(F\). Wynik podaj bez zaokrąglania.
Abiturient jednego z liceów zestawił w tabeli oceny ze swojego świadectwa ukończenia szkoły.
Mediana przedstawionego zestawu danych jest równa
| Ocena | 6 | 5 | 4 | 3 | 2 |
| Liczba ocen | 2 | 3 | 5 | 5 | 1 |
A.\( 3 \)
B.\( 3{,}5 \)
C.\( 4 \)
D.\( 4{,}5 \)
Liczba \(x\) jest dodatnia. Mediana zestawu czterech liczb: \(1+x,\ 1+2x,\ 4+3x,\ 1\), jest równa \(10\). Wtedy
A.\( x=6 \)
B.\( x=5{},5 \)
C.\( x=2{,}5 \)
D.\( x=1 \)
Sześciowyrazowy ciąg liczbowy \((1,\ 2,\ 2x,\ x+2,\ 5,\ 6)\) jest niemalejący. Mediana wyrazów tego ciągu jest równa \(4\). Wynika stąd, że
A.\( x=1 \)
B.\( x=\frac{3}{2} \)
C.\( x=2 \)
D.\( x=\frac{8}{3} \)
Na diagramie poniżej przedstawiono ceny pomidorów w szesnastu wybranych sklepach. 

Uzupełnij tabelę. Wpisz w każdą pustą komórkę tabeli właściwą odpowiedź, wybraną spośród oznaczonych literami A–E.
| 1. | Mediana ceny kilograma pomidorów w tych wybranych sklepach jest równa | |
| 2. | Średnia cena kilograma pomidorów w tych wybranych sklepach jest równa |
A.\( 5{,}80 \)
B.\( 5{,}73 \)
C.\( 5{,}85 \)
D.\( 6{,}00 \)
E.\( 5{,}70 \)
Cztery liczby: \(2, 3, a, 8\), tworzące zestaw danych, są uporządkowane rosnąco. Mediana tego zestawu czterech danych jest równa medianie zestawu pięciu danych: \(5, 3, 6, 8, 2\). Zatem
A.\( a=7 \)
B.\( a=6 \)
C.\( a=5 \)
D.\( a=4 \)
Kąt \(\alpha \) jest kątem ostrym oraz \(\cos \alpha =\frac{2}{3}\). Wykaż, że średnia arytmetyczna liczb: \(a=\sin \alpha \), \(b=\frac{1}{2}\) oraz \(c=\frac{\operatorname{tg} \alpha }{3}\) jest równa \(\frac{\sqrt{5}+1}{6}\).
Ciąg arytmetyczny \((a_n)\) jest określony dla każdej liczby naturalnej \(n\ge1\). Różnicą tego ciągu jest liczba \(r = -4\), a średnia arytmetyczna początkowych sześciu wyrazów tego ciągu: \(a_1\), \(a_2\), \(a_3\), \(a_4\), \(a_5\), \(a_6\), jest równa \(16\).
Oblicz pierwszy wyraz tego ciągu.
Oblicz liczbę \(k\), dla której \(a_k = -78\).
Tematy nadrzędne