Zbiór zadań - równoległoboki i trapezy
Poziom podstawowy
Zadanie 1. (1 pkt)
Przekątne równoległoboku mają długości \(4\) i \(8\), a kąt między tymi przekątnymi ma miarę \(30^\circ \). Pole tego równoległoboku jest równe
A.\( 32 \)
B.\( 16 \)
C.\( 12 \)
D.\( 8 \)
Zadanie 2. (1 pkt)
W równoległoboku \(ABCD\), przedstawionym na rysunku, kąt \(\alpha \) ma miarę \(70^\circ\).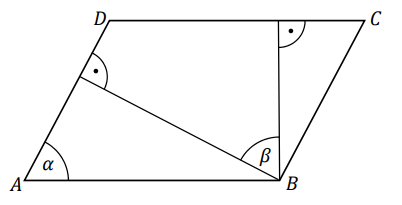 
Wtedy kąt \(\beta\) ma miarę
Wtedy kąt \(\beta\) ma miarę A.\( 80^\circ \)
B.\( 70^\circ \)
C.\( 60^\circ \)
D.\( 50^\circ \)
Zadanie 3. (1 pkt)
Różnica miar dwóch sąsiednich kątów wewnętrznych równoległoboku jest równa \(80^\circ\). Kąt rozwarty tego równoległoboku ma miarę
A.\( 120^\circ \)
B.\( 125^\circ \)
C.\( 130^\circ \)
D.\( 135^\circ \)
Zadanie 4. (1 pkt)
Dany jest romb o boku długości \(4\) i kącie rozwartym \(150^\circ\). Pole tego rombu jest równe
A.\( 8 \)
B.\( 12 \)
C.\( 8\sqrt{3} \)
D.\( 16 \)
Zadanie 5. (1 pkt)
W romb o boku \(2\sqrt{3}\) i kącie \(60^\circ \) wpisano okrąg. Promień tego okręgu jest równy
A.\( 3 \)
B.\( \frac{1}{2} \)
C.\( \frac{3}{4} \)
D.\( \frac{3}{2} \)
Zadanie 6. (1 pkt)
Wysokość rombu jest równa \(12\), a jego pole jest równe \(180\). Sinus kąta ostrego rombu wynosi:
A.\( 0{,}4 \)
B.\( 0{,}6 \)
C.\( 0{,}75 \)
D.\( 0{,}8 \)
Zadanie 7. (1 pkt)
W trapezie równoramiennym \(ABCD\) podstawy \(AB\) i \(CD\) mają długości równe odpowiednio \(a\) i \(b\) (przy czym \(a\gt b\)). Miara kąta ostrego trapezu jest równa \(30^\circ \). Wtedy wysokość tego trapezu jest równa
A.\( \frac{a-b}{2}\cdot \sqrt{3} \)
B.\( \frac{a-b}{6}\cdot \sqrt{3} \)
C.\( \frac{a+b}{2} \)
D.\( \frac{a+b}{4} \)
Zadanie 8. (2 pkt)
Na rysunku przedstawiono trapez \(ABCD\) oraz zaznaczono wysokości \(DE\) i \(CF\) tego trapezu. Punkt \(F\) jest środkiem podstawy \(AB\), a punkt \(E\) dzieli tę podstawę w stosunku \(2:5\). Wykaż, że punkt przecięcia wysokości \(CF\) z przekątną \(DB\) dzieli tę przekątną w stosunku \(3:7\), licząc od wierzchołka \(D\). 
Zadanie 9. (2 pkt)
Rysunek przedstawia trapez równoramienny \(ABCD\) opisany na okręgu o środku \(S\) i promieniu \(r=\frac{\sqrt{91}}{2}\). Dolna podstawa trapezu jest o \(6\) dłuższa od górnej podstawy. Oblicz obwód trapezu \(ABCD\). 
Zadanie 10. (2 pkt)
W trapezie prostokątnym \(ABCD\) dłuższa podstawa \(AB\) ma długość \(8\). Przekątna \(AC\) tego trapezu ma długość \(4\) i tworzy z krótszą podstawą trapezu kąt o mierze \(30^\circ\) (zobacz rysunek). Oblicz długość przekątnej \(BD\) tego trapezu. 
Zadanie 11. (2 pkt)
W równoległoboku \(ABCD\) punkt \(E\) jest środkiem boku \(BC\). Z wierzchołka \(D\) poprowadzono prostą przecinającą bok \(BC\) w punkcie \(E\). Proste \(AB\) i \(DE\) przecinają się w punkcie \(F\) (zobacz rysunek). Wykaż, że punkt \(B\) jest środkiem odcinka \(AF\). 
Zadanie 12. (2 pkt)
Dany jest trapez prostokątny \(ABCD\) o podstawach \(AB\) i \(CD\) oraz wysokości \(AD\). Dwusieczna kąta \(ABC\) przecina ramię \(AD\) w punkcie \(E\) oraz dwusieczną kąta \(BCD\) w punkcie \(F\) (zobacz rysunek). 
Wykaż, że w czworokącie \(CDEF\) sumy miar przeciwległych kątów są sobie równe.
Wykaż, że w czworokącie \(CDEF\) sumy miar przeciwległych kątów są sobie równe.Zadanie 13. (4 pkt)
W trapezie prostokątnym \(ABCD\) dłuższa podstawa \(AB\) ma długość \(7{,}5\). Krótsza przekątna \(AC\) ma długość równą \(6\) i dzieli trapez na dwa trójkąty prostokątne (zobacz rysunek).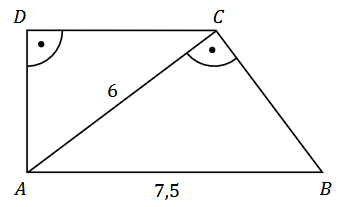 
Oblicz pole trapezu \(ABCD\). Zapisz obliczenia.
Zadanie 14. (5 pkt)
Dany jest trapez prostokątny \(ABCD\) taki, że kąty przy wierzchołkach \(A\) i \(D\) są proste oraz \(|AB|=10\), \(|DC|=6\), a przekątna \(AC\) jest dwa razy dłuższa od ramienia \(DA\). Na podstawie \(AB\) obrano taki punkt \(X\), że \(|CX|=|CB|\) (zobacz rysunek). Oblicz sinus kąta \(XCB\). 
Tematy nadrzędne