Zbiór zadań - przekształcenia wykresów funkcji
Poziom podstawowy
Dane są funkcje \(f(x) = 3^x\) oraz \(g(x) = f(-x)\), określone dla wszystkich liczb rzeczywistych \(x\). Punkt wspólny wykresów funkcji \(f\) i \(g\)
A.nie istnieje
B.ma współrzędne \((1, 0)\).
C.ma współrzędne \((0, 1)\).
D.ma współrzędne \((0, 0)\).
Wykres funkcji \(f(x)=-3^x\) przesunięto równolegle wzdłuż osi \(OX\) o dwie jednostki w prawo i otrzymano wykres funkcji \(y=g(x)\). Wówczas:
A.\( g(x)=-3^x+2 \)
B.\( g(x)=-3^{x+2} \)
C.\( g(x)=-3^x-2 \)
D.\( g(x)=-3^{x-2} \)
Funkcja liniowa \(f\) jest określona wzorem \(f(x)=-2x+4\). Wykres funkcji \(f\) przesunięto wzdłuż osi \(Ox\) o \(2\) jednostki w lewo (tzn. przeciwnie do zwrotu osi), w wyniku czego otrzymano wykres funkcji \(g\). Funkcja \(g\) jest określona wzorem
A.\( g(x)=-2x+2 \)
B.\( g(x)=-2x \)
C.\( g(x)=-2x+6 \)
D.\( g(x)=-2x+8 \)
Dana jest funkcja \(y=f(x)\), której wykres przedstawiono w kartezjańskim układzie współrzędnych \((x,y)\) na rysunku. 
Ta funkcja jest określona dla \(x\in [-3,5]\). Funkcje \(g\) oraz \(h\) są określone za pomocą funkcji \(f\) następująco: \[y=g(x)=f(x+2)\qquad y=h(x)=f(-x)\] Na rysunkach A–F przedstawiono wykresy różnych funkcji – w tym wykresy funkcji \(g\) oraz \(h\). 
Ta funkcja jest określona dla \(x\in [-3,5]\). Funkcje \(g\) oraz \(h\) są określone za pomocą funkcji \(f\) następująco: \[y=g(x)=f(x+2)\qquad y=h(x)=f(-x)\] Na rysunkach A–F przedstawiono wykresy różnych funkcji – w tym wykresy funkcji \(g\) oraz \(h\). Każdej z funkcji \(y=g(x)\) oraz \(y=h(x)\) przyporządkuj jej wykres. Wpisz obok symboli funkcji w tabeli poniżej właściwe odpowiedzi wybrane spośród A–F.
Na rysunku 1. przedstawiono wykres funkcji \(f\) określonej na zbiorze \(\langle -4,5\rangle \). 
Funkcję \(g\) określono za pomocą funkcji \(f\). Wykres funkcji \(g\) przedstawiono na rysunku 2. 
Wynika stąd, że
Funkcję \(g\) określono za pomocą funkcji \(f\). Wykres funkcji \(g\) przedstawiono na rysunku 2. Wynika stąd, że A.\( g(x)=f(x)-2 \)
B.\( g(x)=f(x-2) \)
C.\( g(x)=f(x)+2 \)
D.\( g(x)=f(x+2) \)
Na rysunku przedstawiono wykres funkcji \(f\) określonej na zbiorze \(\langle -2, 5)\).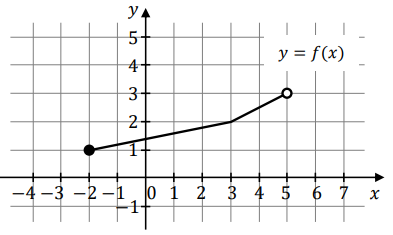 
Funkcja \(g\) jest określona za pomocą funkcji \(f\) następująco: \(g(x) = f(x-1)\). Wykres funkcji \(g\) można otrzymać poprzez odpowiednie przesunięcie wykresu funkcji \(f\). Dziedziną funkcji \(g\) jest zbiór
Funkcja \(g\) jest określona za pomocą funkcji \(f\) następująco: \(g(x) = f(x-1)\). Wykres funkcji \(g\) można otrzymać poprzez odpowiednie przesunięcie wykresu funkcji \(f\). Dziedziną funkcji \(g\) jest zbiór A.\( \langle 0,2) \)
B.\( \langle -1,6) \)
C.\( \langle -3,4) \)
D.\( \langle 1,3) \)
Na rysunku 1. jest przedstawiony wykres funkcji \(f\), a na rysunku 2. - wykres funkcji \(g\). 
Funkcja \(g\) jest określona wzorem
Funkcja \(g\) jest określona wzorem A.\( g(x)=-f(x) \)
B.\( g(x)=f(-x) \)
C.\( g(x)=f(x)+4 \)
D.\( g(x)=f(x)-4 \)
Wykres funkcji wykładniczej \(f(x)=2^x\) poddano czterem przekształceniom w następującej kolejności:
- Przesunięcie o wektor \(\vec{v}=[3,4]\).
- Symetria względem osi \(OX\).
- Przesunięcie o wektor \(\vec{v}=[0,-1]\).
- Symetria względem osi \(OY\).