Zbiór zadań - podstawy trygonometrii
Poziom podstawowy
Kąt \(\alpha \) jest ostry i \(\sin \alpha=\frac{7}{25}\). Wynika stąd, że
A.\( \cos \alpha=\frac{576}{625} \)
B.\( \cos \alpha=\frac{24}{25} \)
C.\( \cos \alpha=-\sqrt{\frac{24}{25}} \)
D.\( \cos \alpha=\frac{18}{25} \)
Cosinus kąta ostrego \(\alpha \) jest równy \(\frac{12}{13}\). Wtedy
A.\( \sin \alpha =\frac{13}{12} \)
B.\( \sin \alpha =\frac{1}{13} \)
C.\( \sin \alpha =\frac{5}{13} \)
D.\( \sin \alpha =\frac{25}{169} \)
Dany jest kąt o mierze \(\alpha\) taki, że \(\sin\alpha = \frac{4}{5}\) oraz 9\(0^\circ \lt \alpha \lt 180^\circ\).
Oceń prawdziwość poniższych zdań. Zaznacz P, jeśli zdanie jest prawdziwe, albo F - jeśli jest fałszywe.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe. | Dla kąta \(\alpha\) spełnione jest równanie: \(\cos \alpha =-\frac{3}{5}\). | P | F |
| Dla kąta \(\alpha\) spełnione jest równanie: \(|\operatorname{tg} \alpha |=\frac{3}{4}\) | P | F |
Dany jest trójkąt prostokątny \(A B C\), w którym \(|A C|=\sqrt{15}\) i \(|B C|=8\). Na przyprostokątnej \(A B\) leży taki punkt \(D\), że \(|B D|=6\) (zobacz rysunek). 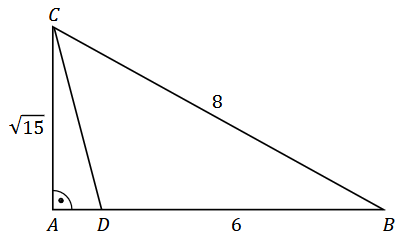

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Sinus kąta ostrego \(A B C\) jest równy A.\(\frac{1}{2}\)
B.\(\frac{7}{8}\)
C.\(\frac{\sqrt{15}}{4}\)
D.\(\frac{\sqrt{15}}{8}\)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Tangens kąta ostrego \(ADC\) jest równy A.\(\sqrt{15}\)
B.\(\frac{1}{2}\)
C.\(\frac{7}{8}\)
D.\(\frac{\sqrt{15}}{8}\)
Kąt \(\alpha \in (0^\circ , 180^\circ )\) oraz wiadomo, że \(\sin \alpha \cdot \cos \alpha =-\frac{3}{8}\). Wartość wyrażenia \((\cos \alpha -\sin \alpha )^2+2\) jest równa
A.\( \frac{15}{4} \)
B.\( \frac{9}{4} \)
C.\( \frac{27}{8} \)
D.\( \frac{21}{8} \)
Dany jest trójkąt prostokątny o kątach ostrych \(\alpha \) i \(\beta \) (zobacz rysunek).  Wyrażenie \(2\cos \alpha -\sin \beta\) jest równe
Wyrażenie \(2\cos \alpha -\sin \beta\) jest równe
 Wyrażenie \(2\cos \alpha -\sin \beta\) jest równe
Wyrażenie \(2\cos \alpha -\sin \beta\) jest równe A.\( 2\sin \beta \)
B.\( \cos \alpha \)
C.\( 0 \)
D.\( 2 \)
Kąt o mierze \(\alpha\) jest rozwarty oraz \(\sin \alpha=\frac{\sqrt{3}}{4}\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Cosinus kąta o mierze \(\alpha\) jest równy A.\(\left(-\frac{\sqrt{13}}{4}\right)\)
B.\(\left(-\frac{1}{2}\right)\)
C.\(\frac{1}{2}\)
D.\(\frac{\sqrt{13}}{4}\)
Kąt \(\alpha \) jest ostry i \(\cos \alpha =\sqrt{2}-1\). Wtedy wyrażenie \(\frac{1}{|\sin^2 \alpha- 2\cos \alpha-1|}\) jest równe
A.\( -1 \)
B.\( 0 \)
C.\( 1 \)
D.\( \frac{\sqrt{2}}{2} \)
Dla każdego kąta ostrego \(\alpha \) iloczyn \(\frac{\cos \alpha }{1-\sin^{2} \alpha }\cdot \frac{1-\cos^{2} \alpha }{\sin \alpha }\) jest równy
A.\( \sin \alpha \)
B.\( \operatorname{tg} \alpha \)
C.\( \cos \alpha \)
D.\( \sin^{2} \alpha \)
Kąt \(\alpha\) jest ostry oraz \(4\operatorname{tg} \alpha =3\sin^{2} \alpha +3\cos^{2} \alpha \).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Tangens kąta \(\alpha\) jest równy A.\( \frac{3}{4} \)
B.\( \frac{4}{3} \)
C.\( \frac{1}{4} \)
D.\( 4 \)
Liczba \(\cos 12^\circ \cdot \sin 78^\circ +\sin 12^\circ \cdot \cos 78^\circ \) jest równa
A.\( \frac{1}{2} \)
B.\( \frac{\sqrt{2}}{2} \)
C.\( \frac{\sqrt{3}}{2} \)
D.\( 1 \)
W trójkącie \(ABC\) dane są długości dwóch boków \(|AB| = 12\), \(|BC| = 8\) oraz miara kąta \(|\sphericalangle ABC| = 60^\circ\).
Oblicz długość środkowej tego trójkąta, poprowadzonej z wierzchołka \(A\).
Kąt \(\alpha \) jest ostry i \((\sin \alpha +\cos \alpha )^2=\frac{3}{2}\). Oblicz wartość wyrażenia \(\sin \alpha \cdot \cos \alpha \).
Kąt \(\alpha \) jest ostry i spełniona jest równość \(\sin \alpha +\cos \alpha =\frac{\sqrt{7}}{2}\). Oblicz wartość wyrażenia \((\sin \alpha -\cos \alpha )^2\).
Kąt \(\alpha \) jest ostry i \(\sin \alpha +\cos \alpha =\sqrt{2}\). Oblicz wartość wyrażenia \(\operatorname{tg} \alpha +\frac{1}{\operatorname{tg} \alpha }\).
Kąt \(\alpha \) jest ostry i spełniona jest równość \(\sin \alpha +\cos \alpha =\sqrt{\sqrt{3}}\). Udowodnij, że istnieje liczba całkowita \(k\), taka, że \(\frac{\sin^2 \alpha +\sin^2 (90^\circ +\alpha)}{\sin \alpha \cos \alpha} = k\sqrt{3}+k\).
Kąt \(\alpha \) jest ostry i \(\sin \alpha + \cos \alpha = \frac{7}{5}\). Oblicz wartość wyrażenia \(2\sin \alpha \cos\alpha\).
Dany jest trójkąt \(ABC\) o bokach długości: \(|AB| = 4\), \(|BC| = 5\), \(|AC| = 6\).
Oblicz sinus najmniejszego kąta wewnętrznego trójkąta \(ABC\).
Dany jest prostokąt \(ABCD\), w którym \(|AD| = 2\). Kąt \(BDA\) ma miarę \(\alpha\), taką, że \(\operatorname{tg} \alpha = 2\). Przekątna \(BD\) i prosta przechodząca przez wierzchołek \(C\) prostopadła do \(BD\) przecinają się w punkcie \(E\) (zobacz rysunek). 

Oblicz długość odcinka \(CE\).
Wierzchołki \(A\) i \(C\) trójkąta \(ABC\) leżą na okręgu o promieniu \(r\). Środek \(S\) tego okręgu leży na boku \(AB\) tego trójkąta (zobacz rysunek poniżej). Długości boków \(AB\) i \(AC\) są równe odpowiednio \(|AB| = 3r\) oraz \(|AC| = \sqrt{3}r\). 

Oblicz miary wszystkich kątów wewnętrznych trójkąta \(ABC\).
Tematy nadrzędne