Zbiór zadań - odczytywanie informacji z wykresu funkcji
Poziom podstawowy
Na rysunku przedstawiono wykres funkcji \(f\). 
Iloczyn \(f(-3)\cdot f(0)\cdot f(4)\) jest równy
Iloczyn \(f(-3)\cdot f(0)\cdot f(4)\) jest równy A.\( (-12) \)
B.\( (-8) \)
C.\( 0 \)
D.\( 16 \)
Dana jest funkcja \(y=f(x)\), której wykres przedstawiono w kartezjańskim układzie współrzędnych \((x,y)\) na rysunku. 
Ta funkcja jest określona dla każdej liczby rzeczywistej \(x\in [-5,8]\).
Ta funkcja jest określona dla każdej liczby rzeczywistej \(x\in [-5,8]\).Zapisz w miejscu wykropkowanym poniżej zbiór rozwiązań nierówności: \[f(x)\gt 2\]
Zapisz w miejscu wykropkowanym poniżej maksymalny przedział lub maksymalne przedziały, w których funkcja \(f\) jest malejąca.
Uzupełnij zdanie. Wpisz odpowiednie liczby w wykropkowanych miejscach, aby zdanie było prawdziwe.
Największa wartość funkcji \(f\) jest równa liczbie ............... , a najmniejsza wartość funkcji \(f\) jest równa liczbie .......................Funkcja \(f\) jest określona następująco: \[ f(x)= \begin{cases}3 & \text { dla } x \in(-4,-2] \\ -x+1 & \text { dla } x \in(-2,2] \\ x-3 & \text { dla } x \in(2,4]\end{cases} \] Wykres funkcji \(y=f(x)\) przedstawiono w kartezjańskim układzie współrzędnych \((x, y)\) na rysunku poniżej.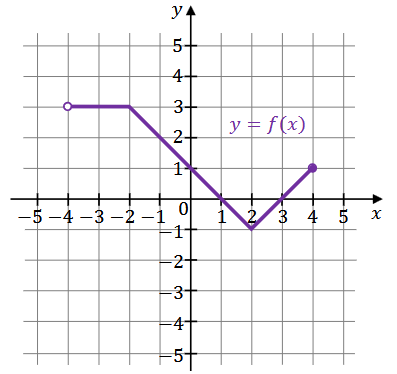 
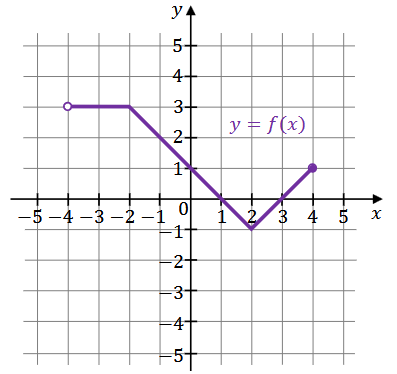
Uzupełnij zdania. Wpisz odpowiednie przedziały w wykropkowanych miejscach, aby zdania były prawdziwe.
- Dziedziną funkcji \(f\) jest przedział .............. .
- Zbiorem wartości funkcji \(f\) jest przedział .............. .
- Zbiorem wszystkich argumentów, dla których funkcja \(f\) przyjmuje wartości ujemne, jest przedział .............. .
- Zbiorem wszystkich argumentów, dla których funkcja \(f\) przyjmuje największą wartość, jest przedział .............. .
Funkcja \(f\) jest określona następująco: \[ f(x)= \begin{cases}x+4 & \text { dla } x \in[-8,0] \\ 4 & \text { dla } x \in(0,4] \\ -2 x+12 & \text { dla } x \in(4,6)\end{cases} \] Wykres funkcji \(y=f(x)\) przedstawiono w kartezjańskim układzie współrzędnych \((x, y)\) na rysunku poniżej.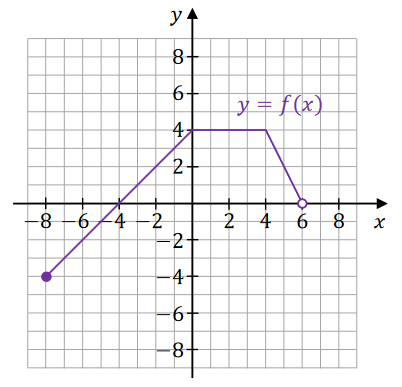 
Uzupełnij zdania. Wpisz odpowiednie przedziały w wykropkowanych miejscach tak, aby zdania były prawdziwe.
- Dziedziną funkcji \(f\) jest przedział \(............\) .
- Zbiorem wartości funkcji \(f\) jest przedział \(............\) .
- Zbiorem wszystkich argumentów, dla których funkcja \(f\) przyjmuje wartości nieujemne, jest przedział \(............\) .
- Zbiorem wszystkich rozwiązań równania \(f(x)=4\) jest przedział \(............\) .
Rysunek przedstawia wykres pewnej funkcji \( y=f(x) \), określonej dla \( x \in \langle -4,4 \rangle \). 
Zbiór wszystkich argumentów, dla których funkcja \( f \) przyjmuje wartości niedodatnie, to zbiór
Zbiór wszystkich argumentów, dla których funkcja \( f \) przyjmuje wartości niedodatnie, to zbiór A.\(\langle 0,3 )\cup ( 3,4 \rangle \)
B.\(\langle -4,-3 \rangle\cup \langle 0,4 \rangle \)
C.\((-4,-3)\cup (0,3)\cup (3,4) \)
D.\((-2,1)\cup (3,4) \)
Największą wartością funkcji \( f \) jest 
A.\(3 \)
B.\(0 \)
C.\(-3 \)
D.\(8 \)
Na rysunku przedstawiono wykres funkcji \(f\).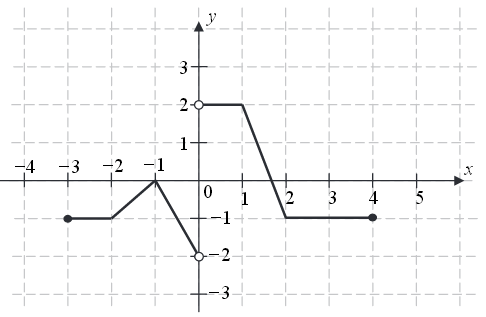 
Zbiorem wartości funkcji \(f\) jest
Zbiorem wartości funkcji \(f\) jest A.\( (-2,2\rangle \)
B.\( \langle -2,2\rangle \)
C.\( \langle -2,2) \)
D.\( (-2,2) \)
Na rysunku przedstawiono wykres pewnej funkcji \(f\). Maksymalny przedział, w którym funkcja \(f\) jest rosnąca, to: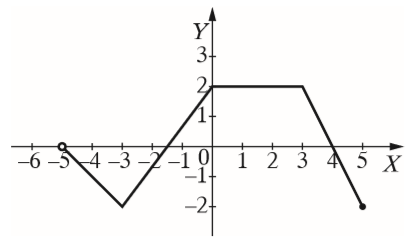 
A.\( \langle -2;0 \rangle \)
B.\( \langle -2;2 \rangle \)
C.\( \langle -3;2 \rangle \)
D.\( \langle -3;0 \rangle \)
Rysunek przedstawia wykres funkcji \(f\) zbudowany z \(6\) odcinków, przy czym punkty \(B=(2,-1)\) i \(C=(4,-1)\) należą do wykresu funkcji. 
Równanie \(f(x)=-1\) ma
Równanie \(f(x)=-1\) ma A.dokładnie jedno rozwiązanie.
B.dokładnie dwa rozwiązania.
C.dokładnie trzy rozwiązania.
D.nieskończenie wiele rozwiązań.
Funkcja, której wykres przedstawiono na rysunku jest rosnąca: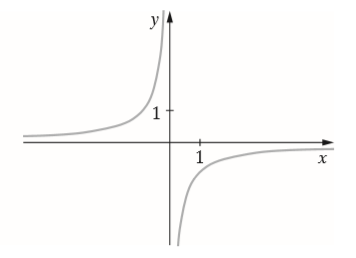 
A.tylko w przedziale \( (-\infty ,0) \)
B.tylko w przedziale \( (0,+\infty ) \)
C.w \( \mathbb{R} \backslash \{0\} \)
D.w każdym z przedziałów \( (-\infty ,0) \) i \((0, +\infty )\)
Na wykresie przedstawiono wykres funkcji \(f\)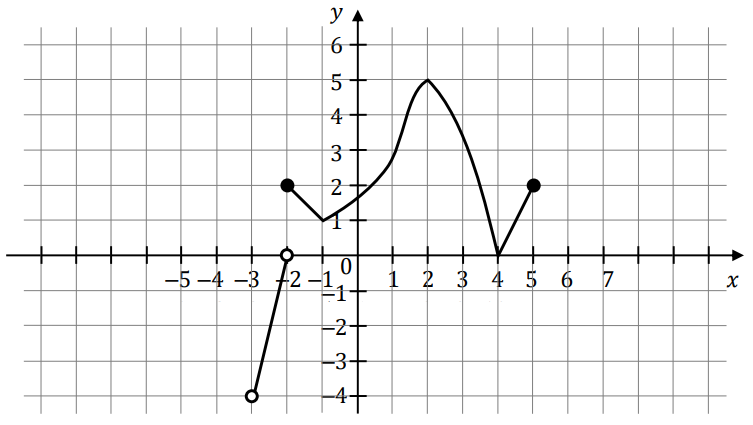 
Wskaż zdanie prawdziwe.
Wskaż zdanie prawdziwe. A.Dziedziną funkcji \(f\) jest przedział \((−4, 5)\).
B.Funkcja \(f\) ma dwa miejsca zerowe.
C.Funkcja \(f\) dla argumentu \(1\) przyjmuje wartość \((−1)\).
D.Zbiorem wartości funkcji \(f\) jest przedział \((−4, 5\rangle \).
Tematy nadrzędne