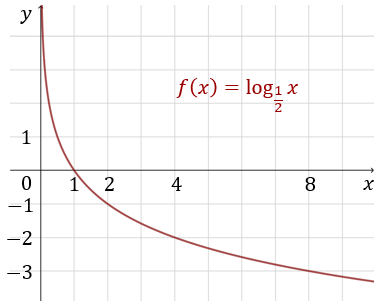Zbiór zadań - funkcja wykładnicza i logarytmiczna

Drukuj

Poziom podstawowy

Dane są funkcje \(f(x) = \left(\frac{1}{2}\right)^x\) oraz \(g(x) = -f(-x)\), określone dla wszystkich liczb rzeczywistych \(x\). Punkt wspólny wykresów funkcji \(f\) i \(g\)

A.nie istnieje

B.ma współrzędne \((1, 0)\).

C.ma współrzędne \((0, 1)\).

D.ma współrzędne \((0, 0)\).

Na rysunku przedstawiono fragment wykresu funkcji wykładniczej \(f\) określonej wzorem \(f(x)=a^x\). Punkt \(A=(1,2)\) należy do wykresu funkcji.

Podstawa \(a\) potęgi jest równa

A.\( -\frac{1}{2} \)

B.\( \frac{1}{2} \)

C.\( -2 \)

D.\( 2 \)

Do wykresu funkcji wykładniczej \(f(x)=\left(\frac{1}{4}\right)^x\) należy punkt

A.\( A=\left(-\frac{1}{2},-2\right) \)

B.\( A=\left(-\frac{1}{2},2\right) \)

C.\( A=\left(2,\frac{1}{2}\right) \)

D.\( A=\left(2,-\frac{1}{2}\right) \)

Funkcja logarytmiczna \(f\) jest określona wzorem \(f(x)=\log _{6} x\) dla każdej dodatniej liczby rzeczywistej \(x\).

Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.

Wartość funkcji \(f\) dla argumentu \(36\) jest równa \(6\).	P	F
Funkcja \(f\) jest rosnąca.	P	F

Wirus rozprzestrzenia się w tempie wykładniczym zwiększając liczbę zarażonych osób dwukrotnie przez okres \(4\) dni. Jeżeli 3 kwietnia 2020 liczba zarażonych osób wyniosła \(100\), to ile osób będzie zarażonych 27 kwietnia 2020 (zakładamy, że tempo rozprzestrzeniania się wirusa jest niezmienne przez cały rozważany okres czasu)?

A.\( 6\cdot 10^2 \)

B.\( 2{,}4\cdot 10^3 \)

C.\( 6{,}4\cdot 10^3 \)

D.\( 100\cdot 2^{23} \)

Do wykresu funkcji wykładniczej, określonej dla każdej liczby rzeczywistej \(x\) wzorem \(f(x) = a^x\) (gdzie \(a \gt 0\) i \(a \ne 1\)), należy punkt \(P = (2, 9)\). Oblicz \(a\) i zapisz zbiór wartości funkcji \(g\), określonej wzorem \(g(x) = f(x) - 2\).

\(a = 3\), zbiór wartości: \((-2, +\infty )\)

Narysuj wykres funkcji \(f(x)=2^x-3\). Podaj zbiór wartości tej funkcji.

\(ZW=(-3,+\infty )\)

Czas \(T\) połowicznego rozpadu izotopu promieniotwórczego to czas, po którym liczba jąder danego izotopu (a zatem i masa tego izotopu) zmniejsza się o połowę – tzn. połowa jąder danego izotopu przemienia się w inne jądra. Liczba jąder \(N(t)\) izotopu promieniotwórczego pozostających w próbce po czasie \(t\), licząc od chwili \(t_0 = 0\), wyraża się zależnością wykładniczą: \[N(t)=N_0\left(\frac{1}{2}\right)^{\frac{t}{T}}\] gdzie \(N_0\) jest liczbą jąder izotopu promieniotwórczego w chwili początkowej \(t_0 = 0\).

Na poniższych rysunkach 1.-4. przedstawiono wykresy różnych zależności.

Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych.

Wykres zależności wykładniczej \(N(t)\) - opisanej we wstępie do zadania - przedstawiono na

A.rysunku 1.

B.rysunku 2.

C.rysunku 3.

D.rysunku 4.

Czas połowicznego rozpadu węgla \(^{14}\text{C}\) to około \(5700\) lat. Naukowcy oszacowali za pomocą datowania radiowęglowego, że masa izotopu węgla \(^{14}\text{C}\) w pewnym organicznym znalezisku archeologicznym stanowi \(\frac{1}{16}\) masy tego izotopu, jaka utrzymywała się podczas życia organizmu.

Oblicz, ile lat ma opisane znalezisko archeologiczne. Wynik podaj z dokładnością do stu lat.

\(22\ 800\) lat

Czas \(T\) półtrwania leku w organizmie to czas, po którym masa leku w organizmie zmniejsza się o połowę - po przyjęciu jednorazowej dawki.
Przyjmij, że po przyjęciu jednej dawki masa \(m\) leku w organizmie zmienia się w czasie zgodnie z zależnością wykładniczą \[m(t)=m_0\cdot \left(\frac{1}{2}\right)^{\frac{t}{T}}\]

gdzie:
\(m_0\) - masa przyjętej dawki leku
\(T\) - czas półtrwania leku
\(t\) - czas liczony od momentu przyjęcia dawki.

W przypadku przyjęcia kilku(nastu) dawek powyższa zależność pozwala obliczyć, ile leku pozostało w danym momencie w organizmie z każdej poprzednio przyjętej dawki. W ten sposób obliczone masy leku z przyjętych poprzednich dawek sumują się i dają informację o całkowitej aktualnej masie leku w organizmie.

Pacjent otrzymuje co \(4\) dni o tej samej godzinie dawkę \(m_0=100\) mg leku \(L\). Czas półtrwania tego leku w organizmie jest równy \(T = 4\) doby.

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Wykres zależności masy \(M\) leku \(L\) w organizmie tego pacjenta od czasu \(t\), liczonego od momentu przyjęcia przez pacjenta pierwszej dawki, przedstawiono na rysunku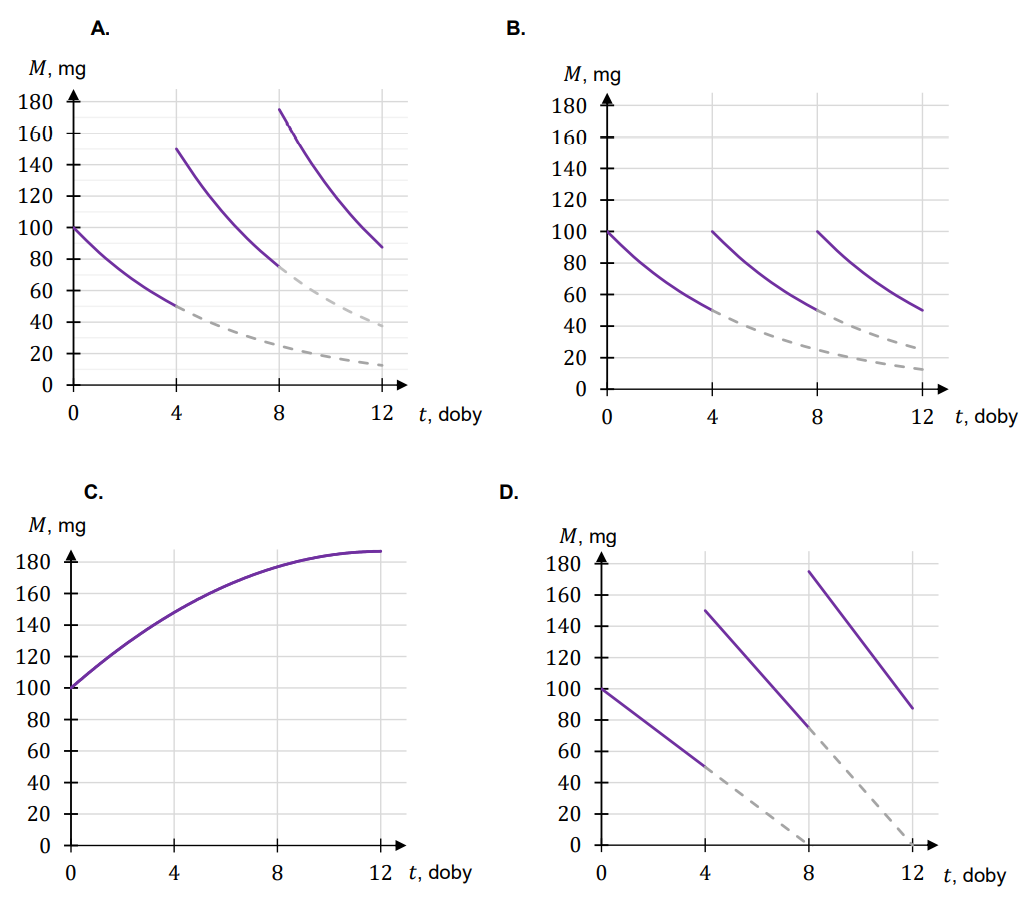

Oblicz masę leku \(L\) w organizmie tego pacjenta tuż przed przyjęciem jedenastej dawki tego leku. Wynik podaj w zaokrągleniu do \(0{,}1\) mg.
Zapisz obliczenia.

\(99{,}9\)

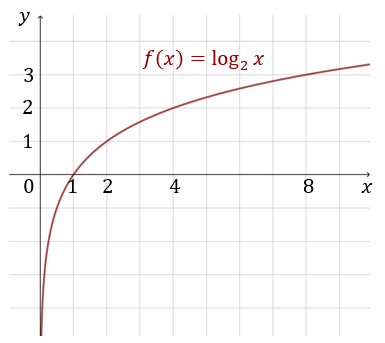
Dana jest funkcja \(f(x)=\log_2 x\), gdzie \(x \in R_{+}\).

Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.

Funkcja \(f\) ma miejsce zerowe mniejsze od \(2\).	P	F
Prawdziwa jest nierówność: \(f(\sqrt{2}) \gt 0\).	P	F

Sprawdzamy, czy funkcja ma miejsce zerowe, czyli czy istnieje argument \(x\), dla którego zeruje się wzór funkcji: \[\log_2 x = 0\\[6pt] x = 2^0\\[6pt] x= 1 \] Pamiętamy, że dziedziną logarytmu jest \(x\gt 0\). Zatem rozwiązanie \(x=1\) należy do dziedziny.
Zatem funkcja ma miejsce zerowe \(x=1\).
Można było to też stwierdzić na podstawie wykresu:

Funkcja \(f(x)=\log_2 x\) jest rosnąca i \(f(1) = 0\), zatem \(f(\sqrt{2}) \gt 0\).

Czyli oba zdania są prawdziwe: PP.

Dana jest funkcja \(f(x)=\log _{\frac{1}{2}} x\), gdzie \(x \in R_{+}\).

Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.

Funkcja \(f\) jest rosnąca.	P	F
Zachodzi nierówność: \(f(1) \lt f(\sqrt{2})\).	P	F

Funkcja logarytmiczna \(y=\log_ax\) jest rosnąca, jeśli \(a\gt 1\), a malejąca, jeśli \(0 \lt a \lt 1\).
Zatem funkcja \(f(x)=\log _{\frac{1}{2}} x\) jest malejąca (bo ma podstawę równą \(\frac{1}{2}\), czyli mniejszą od \(1\)), stąd pierwsze zdanie jest fałszywe.

Przypomnijmy wykres tej funkcji:

Ponieważ funkcja jest malejąca, zatem: \(f(1) \gt f(\sqrt{2})\). Zatem drugie zdanie jest fałszywe.

Można było też obliczyć wartości funkcji: \[f(1)=\log _{\frac{1}{2}} 1 = 0\] oraz: \[f(\sqrt{2})=\log _{\frac{1}{2}} \sqrt{2} = c\\[6pt] \left(\frac{1}{2}\right)^c=\sqrt{2}\\[6pt] \left(2\right)^{-c}=2^{\frac{1}{2}}\\[6pt] -c=\frac{1}{2}\\[6pt] c=-\frac{1}{2} \] Zatem: \[f(\sqrt{2})=-\frac{1}{2}\]

Czyli \(f(1) \gt f(\sqrt{2})\), bo \(0\gt -\frac{1}{2}\).

Czyli oba zdania są fałszywe: FF.

Czas połowicznego rozpadu jodu wynosi \(8\) dni. Jeśli masa początkowa wynosi \(m_0\), to po upływie \(t\) dni masa dana jest za pomocą wzoru: \[ m=m_0 \cdot\left(\frac{1}{2}\right)^{\frac{t}{8}} \] Oblicz ile z masy \(80\) mg próbki jodu zostanie po 16 dniach. Oblicz po ilu dniach z masy \(80\) mg próbki jodu zostanie \(5\) mg.

Po \(16\) dniach zostanie \(20\) mg
Masa próbki \(80\) mg zmaleje do \(5\) mg po \(32\) dniach.

Po \(16\) dniach dla próbki o masie początkowej \(80\) mg zostanie:

\(m(16)=80\cdot\left(\frac{1}{2}\right)^{\frac{16}{8}}=80\cdot\left(\frac{1}{2}\right)^2=80\cdot\frac{1}{4}=20\) mg

Teraz obliczymy, po ilu dniach masa próbki \(80\) mg zmaleje do \(5\) mg: \[ \begin{split} 5&=80\cdot \left(\frac{1}{2}\right)^{\frac{t}{8}}\\[6pt] \left(\frac{1}{2}\right)^{\frac{t}{8}}&=\frac{5}{80}\\[6pt] \left(\frac{1}{2}\right)^{\frac{t}{8}}&=\frac{1}{16}\\[6pt] \left(\frac{1}{2}\right)^{\frac{t}{8}}&=\left(\frac{1}{2}\right)^4\\[6pt] \frac{t}{8}&=4\\[6pt] t&=32 \end{split}\] Zatem masa próbki \(80\) mg zmaleje do \(5\) mg po \(32\) dniach.

Dana jest funkcja opisująca wykładniczy wzrost liczby komórek: \[ N(t)=N_0\cdot 2^{\frac{t}{T_d}}, \] gdzie \(N_0\) to liczba początkowa, a \(T_d\) to czas podwajania liczby komórek w godzinach. W eksperymencie początkowa liczba komórek wynosi \(500\), a czas podwajania \(T_d=4\) godziny.

Oblicz liczbę komórek po \(12\) godzinach.
Oblicz, po ilu godzinach liczba komórek osiągnie \(8000\).

\(4000\)
Po \(16\) godzinach

W podanym eksperymencie mamy \(N=500\) oraz \(T_d=4\), zatem wzór funkcji to: \[N(t)=500\cdot 2^{\frac{t}{4}}\]

Do wyrażenia \(N(t)=500\cdot 2^{\frac{t}{4}}\) podstawiamy \(t=12\):
\(N(12)=500\cdot 2^{\frac{12}{4}}=500\cdot 2^3=500\cdot 8=4000\)
Obliczamy, po ilu godzinach \(N(t)=8000\): \[ \begin{split} 8000&=500\cdot 2^{\frac{t}{4}}\\[6pt] 2^{\frac{t}{4}}&=\frac{8000}{500}\\[6pt] 2^{\frac{t}{4}}&=16\\[6pt] 2^{\frac{t}{4}}&=2^4\\[6pt] \frac{t}{4}&=4\\[6pt] t&=16\\[6pt] \end{split} \] Zatem po \(16\) godzinach liczba komórek osiągnie \(8000\).

W pewnym eksperymencie chemicznym stopień zaawansowania reakcji określony jest przez funkcję: \[ S(t)=\log_5(t) \] gdzie \(t\) oznacza czas reakcji (w minutach). Wykonaj następujące zadania:

Oblicz stopień zaawansowania reakcji dla \(t=125\) minut.
Oblicz, po ilu minutach stopień zaawansowania reakcji osiągnie wartość \(4\).

\(S(125)=3\)
\(t=625\)

Obliczamy wartość funkcji \(S(t)\) dla \(t=125\): \[ S(125) = \log_5 125 = 3 \]
Obliczamy czas \(t\) dla \(S(t)=4\): \[ \begin{split} 4 &= \log_5 t\\[6pt] t &= 5^4\\[6pt] t &= 625 \end{split} \]

Poziom dźwięku wyrażony w dB w zależności od natężenia dźwięku \(I\) wyraża się wzorem: \[ L(I)=10\log\left(\frac{I}{I_0}\right) \] gdzie \(I_0=10^{-12}\) [W/m²].

Oblicz poziom dźwięku, gdy \(I=10^{-6}\) [W/m²].
Oblicz natężenie \(I\) (w W/m²), gdy \(L=80\) [dB].

\(60\) dB
\(I=10^{-4} \text{ W/m}^2\)

Funkcja \(L(I)\) dla stałej \(I_0=10^{-12}\) [W/m²] wyraża się wzorem: \[ L(I)=10\log\left(\frac{I}{10^{-12}}\right) \]

Obliczamy wartość funkcji \(L(I)\) dla \(I=10^{-6}\) [W/m²]:
\(L(10^{-6})=10\log\left(\frac{10^{-6}}{10^{-12}}\right)\) \(=10\log\left(10^6\right)\) \(=10\cdot6=60\) [dB]
Obliczmy \(I\), gdy \(L=80\) dB: \[ 80=10\log\left(\frac{I}{10^{-12}}\right)\\[6pt] \log\left(\frac{I}{10^{-12}}\right)=8\\[6pt] \frac{I}{10^{-12}}=10^8\\[6pt] I=10^8\cdot 10^{-12}\\[6pt] I=10^{-4} \text{ W/m}^2 \]