Zbiór zadań - funkcja liniowa
Poziom podstawowy
Dana jest funkcja liniowa \(f\) określona wzorem\(f(x)=ax+b\), gdzie \(a\) i \(b\) są liczbami rzeczywistymi. Wykres funkcji \(f\) przedstawiono w kartezjańskim układzie współrzędnych \((x,y)\) na rysunku poniżej.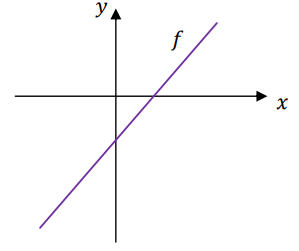 
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Współczynniki \(a\) i \(b\) we wzorze funkcji \(f\) spełniają warunki A.\( a\gt 0 \) i \(b\gt 0\).
B.\( a\gt 0 \) i \(b\lt 0\).
C.\( a\lt 0 \) i \(b\gt 0\).
D.\( a\lt 0 \) i \(b\lt 0\).
Miejscem zerowym funkcji liniowej \(f\) jest liczba 2, a punkt przecięcia wykresu funkcji \(f\) z osią \(O y\) kartezjańskiego układu współrzędnych \((x, y)\) ma współrzędne \((0,4)\) (zobacz rysunek).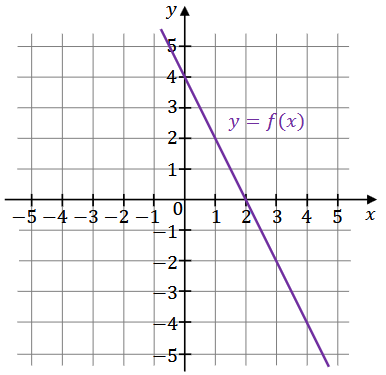 
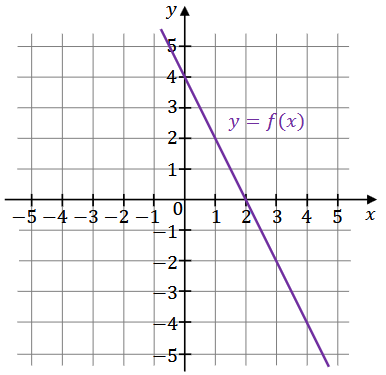
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
| Współczynnik kierunkowy prostej, która jest wykresem funkcji \(f\), jest równy \((-2)\). | P | F |
| Pole trójkąta ograniczonego osiami kartezjańskiego układu współrzędnych \((x, y)\) oraz wykresem funkcji \(f\) jest równe \(8\). | P | F |
Na rysunku przedstawiono fragment wykresu funkcji liniowej \(f\) określonej wzorem \(f(x)=ax+b\). 
Współczynniki \(a\) oraz \(b\) we wzorze funkcji \(f\) spełniają zależność
Współczynniki \(a\) oraz \(b\) we wzorze funkcji \(f\) spełniają zależność A.\( a+b\gt0 \)
B.\( a+b=0 \)
C.\( a\cdot b\gt0 \)
D.\( a\cdot b\lt0 \)
Funkcja liniowa \(f(x)=(a-1)x+3\) osiąga wartość najmniejszą równą \(3\). Wtedy
A.\( a=-1 \)
B.\( a=0 \)
C.\( a=1 \)
D.\( a=3 \)
Punkt \(A=(a,3)\) leży na prostej określonej równaniem \(y=\frac{3}{4}x+6\). Stąd wynika, że
A.\( a=-4 \)
B.\( a=4 \)
C.\( a=\frac{33}{4} \)
D.\( a=\frac{39}{4} \)
Funkcja \(f\) jest określona wzorem \(f(x)=ax+4\) dla każdej liczby rzeczywistej \(x\). Miejscem zerowym tej funkcji jest liczba \((-1)\). Wtedy
A.\( a=-4 \)
B.\( a=1 \)
C.\( a=4 \)
D.\( a=5 \)
Miejscem zerowym funkcji liniowej \(f\) określonej wzorem \(f(x)=-\frac{1}{3}(x+3)+5\) jest liczba
A.\( (-3) \)
B.\( \frac{9}{2} \)
C.\( 5 \)
D.\( 12 \)
Funkcja liniowa \(f\) jest określona wzorem \(f(x)=(a+1)x+11\), gdzie \(a\) to pewna liczba rzeczywista, ma miejsce zerowe równe \(x=\frac{3}{4}\). Stąd wynika, że
A.\( a=-\frac{41}{3} \)
B.\( a=\frac{41}{3} \)
C.\( a=-\frac{47}{3} \)
D.\( a=\frac{47}{3} \)
Funkcja liniowa \(f(x)=(1-m^2)x+m-1\) nie ma miejsc zerowych dla
A.\( m=1 \)
B.\( m=0 \)
C.\( m=-1 \)
D.\( m=-2 \)
Funkcja liniowa \(f\) określona wzorem \(f(x)=(2m-5)x+22\) jest rosnąca dla
A.\( m\gt\frac{2}{5} \)
B.\( m\gt2{,}5 \)
C.\( m\gt0 \)
D.\( m\gt2 \)
Funkcja \(f\) jest określona dla każdej liczby rzeczywistej \(x\) wzorem \(f(x)=(m\sqrt{5}-1)x+3\). Ta funkcja jest rosnąca dla każdej liczby \(m\) spełniającej warunek
A.\( m\gt\frac{1}{\sqrt{5}} \)
B.\( m\gt1-\sqrt{5} \)
C.\( m\lt\sqrt{5}-1 \)
D.\( m\lt\frac{1}{\sqrt{5}} \)
Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych.
W kartezjańskim układzie współrzędnych \((x, y)\) wykresy funkcji liniowych \(f(x)=(2m+7) x+5\) oraz \(g(x)=3x\) nie maja punktów wspólnych dla A.\(m=-2\)
B.\(m=-1\)
C.\(m=1\)
D.\(m=2\)
Prosta \(k\) przechodzi przez punkt \(A=(2,-3)\) i jest nachylona do osi \(Ox\) pod kątem \(45^\circ \) (zobacz rysunek). 
Prosta \(k\) ma równanie
Prosta \(k\) ma równanie A.\( y=x-5 \)
B.\( y=-x-1 \)
C.\( y=-x+5 \)
D.\( y=x+5 \)
Punkty \(P = (-3, 4)\) i \(O = (0, 0)\) leżą na jednej prostej. Kąt \(\alpha \) jest kątem nachylenia tej prostej do osi \(Ox\) (zobacz rysunek). 
Wtedy tangens \(\alpha \) jest równy
Wtedy tangens \(\alpha \) jest równy A.\( -\frac{3}{4} \)
B.\( -\frac{4}{3} \)
C.\( \frac{4}{3} \)
D.\( \frac{3}{4} \)
Funkcja liniowa \(f\) przyjmuje wartość \(2\) dla argumentu \(0\), a ponadto \(f(4)-f(2)=6\). Wyznacz wzór funkcji \(f\).
Dana jest funkcja \(f\) określona wzorem: \[ f(x)=\left\{\begin{array}{cc} 2 x-6 & \text { dla } x \leq 2 \\ x-4 & \text { dla } x\gt 2 \end{array}\right. \]
Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych.
Miejscem zerowym funkcji \(f\) jest liczba A.\( (-6) \)
B.\( (-4) \)
C.\( 3 \)
D.\( 4 \)
Tematy nadrzędne