Matura - najważniejsze wzory spoza tablic

Drukuj

Tablice dostępne na maturze:

Tablice maturalne - formuła 2023

Przed maturą warto dobrze zapoznać się z powyższymi tablicami, żeby na maturze wiedzieć, gdzie szybko znaleźć potrzebną informację.

Poniżej prezentuję wzory i wiadomości, których nie ma w tablicach, a które również bywają przydatne.

Poziom podstawowy

Własności liczb

Cechy podzielności liczb:

przez \(2\), jeśli jest parzysta.

przez \(3\), jeżeli suma jej cyfr dzieli się przez \(3\).

przez \(5\), jeżeli jej ostatnia cyfra dzieli się przez \(5\).

przez \(6\), jeśli jest parzysta i suma jej cyfr jest podzielna przez \(3\).

przez \(9\), jeśli suma jej cyfr tworzy liczbę podzielną przez \(9\).

Sposób zapisywania liczby:

parzystej: \(2k\), gdzie \(k\in \mathbb{Z} \)
nieparzystej: \(2k+1\), gdzie \(k\in \mathbb{Z} \)

Funkcje

Definicje pojęć, których nie ma w tablicach:

dziedzina - to zbiór wszystkich \(x\)-ów funkcji
zbiór wartości - to zbiór wszystkich\(y\)-ów funkcji
miejsce zerowe - to argument \(x\), dla którego funkcja przecina się z osią \(x\)-ów. Gdy mamy wzór funkcji \(f(x) = wzór\), to miejsca zerowe wyliczamy rozwiązując równanie: \[wzór = 0\]
numery ćwiartek w układzie współrzędnych:
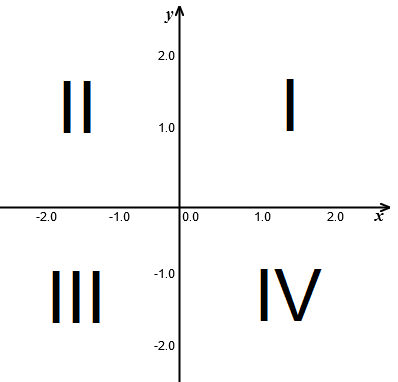
oś odciętych - to oś \(x\)-ów
oś rzędnych - to oś \(y\)-ów

Funkcja kwadratowa

Do informacji, które są podane w tablicach maturalnych warto dodać, że:

Funkcja kwadratowa dana wzorem ogólnym \(f(x)=ax^2+bx+c\) przecina oś \(y\)-ów w wartości równej \(c\) (ponieważ \(f(0)=c\)).
Jeśli funkcja kwadratowa \(f(x)\) ma dwa miejsca zerowe: \(x_1\) oraz \(x_2\), to wierzchołek paraboli \(W=(p,q)\) ma współrzędną \(x\)-ową \(p\) dokładnie po środku między miejscami zerowymi, czyli: \[p=\frac{x_1+x_2}{2}\] Natomiast współrzędną \(q\) można obliczyć zawsze tak: \[q=f(p)\]
Żeby znaleźć minimum lub maksimum funkcji w przedziale \(\langle a,b \rangle \) należy policzyć \(f(a)\) i \(f(b)\) oraz sprawdzić czy współrzędna \(x\)-owa wierzchołka \(p\) należy do przedziału \(\langle a,b \rangle \). Jeśli tak, to policzyć \(f(p)\) i z wartości \(f(a)\), \(f(b)\) i \(f(p)\) wybrać wartość najmniejszą lub największą.

Dokładne omówienie funkcji znajdziesz tutaj: Kurs podstawowy - funkcje.

Ciąg arytmetyczny i geometryczny

Z ciągu arytmetycznego mamy podany w tablicach wzór na \(n\)-ty wyraz postaci: \(a_n=a_1+(n-1)\cdot r\).
Warto znać również wzrór wykorzystujący dowolny \(k\)-ty wyraz zamiast \(1\)-szego: \[a_n=a_k+(n-k)\cdot r\] Podobnie dla ciągu geometrycznego mamy podany wzór: \(a_n = a_1\cdot q^{n-1}\), a można również stosować taki wzór uogólniony: \[a_n = a_k\cdot q^{n-k}\] Dokładne omówienie ciągów znajdziesz tutaj: Kurs podstawowy - ciągi.

Kapitalizacja odsetek

W tablicach maturalnych mamy podany wzór na kapitalizację odsetek: \[K_n = K\cdot \left(1+\frac{p}{100}\right)^n\] Jeżeli w ciągu roku mamy \(k\) kapitalizacji odsetek to stosujemy wzór: \[K_n = K\cdot \left(1+\frac{p}{100\cdot k}\right)^{n\cdot k}\] gdzie:

\(K\) - kapitał początkowy
\(n\) - liczba lat oszczędzania
\(p\) - oprocentowanie w skali roku
\(k\) - liczba kapitalizacji w ciągu roku
\(K_n\) - kapitał zgromadzony po \(n\) latach oszczędzania

Przykłady zastosowania tego wzoru prezentuję na tej stronie.

Geometria płaska

Warto pamiętać często stosowany wzór na przekątną kwadratu: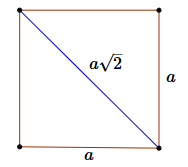

Dla trójkąta równobocznego: wato pamiętać o własności: \[R=2r\] W tablicach maturalnych mamy to podane w postaci: \[R = \frac{2}{3}h\\[6pt] r = \frac{1}{3}h\] gdzie \(h\) - to wysokość trójkąta równobocznego.
Inaczej mówiąc - wysokości w trójkącie równobocznym przecinają się w stosunku \(2:1\).

Dla trójkąta prostokątnego: 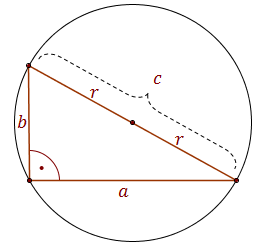warto pamiętać, że środek okręgu opisanego leży dokładnie na środku przeciwprostokątnej.

Własności trójkąta \(30^\circ \), \(60^\circ \), \(90^\circ \):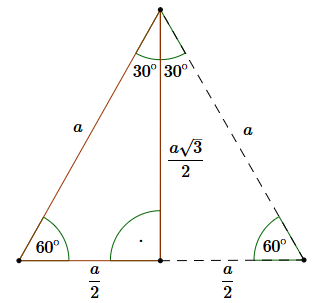

W trapezie zachodzi następująca własność: 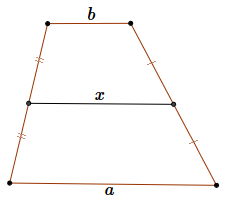Odcinek łączący środki ramion jest równoległy do podstaw i ma długość: \[x=\frac{a+b}{2}\]

Wzór na sumę kątów wewnętrznych w \(n\)-kącie: \[(n-2)\cdot 180\]

Równość odcinków do punktów styczności, w szczególności w przypadku okręgu wpisanego w trójkąt:

Poziom rozszerzony

Zadania dowodowe

W zadaniach dowodowych czasem przydaje się nierówność między średnią arytmetyczną i kwadratową: \[\frac{x+y}{2}\le \sqrt{\frac{x^2+y^2}{2}}\] lub w wersji dla trzech literek: \[\frac{x+y+z}{3}\le \sqrt{\frac{x^2+y^2+z^2}{3}}\]

Geometria płąska

Twierdzenie o dwusiecznej dla dowolnego trójkąta: 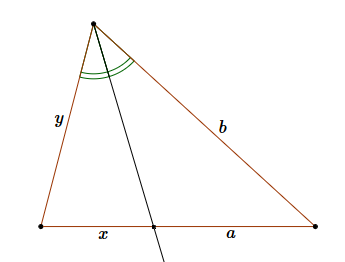\[\frac{x}{y}=\frac{a}{b}\]