Matura 2012 marzec 7

Drukuj

Poziom podstawowy

Szybka nawigacja do zadania numer: 5 10 15 20 25 30 .

Liczbę \(\sqrt{32}\) można przedstawić w postaci

A.\( 8\sqrt{2} \)

B.\( 12\sqrt{3} \)

C.\( 4\sqrt{8} \)

D.\( 4\sqrt{2} \)

Potęga \(\left ( \frac{y}{x} \right )^5\) (gdzie \(x\) i \(y\) są różne od zera) jest równa

A.\( -5\cdot \frac{x}{y} \)

B.\( \left ( \frac{x}{y} \right )^{-5} \)

C.\( \frac{y^5}{x} \)

D.\( -\left ( \frac{x}{y} \right )^5 \)

Liczba \(\log_{3}\frac{1}{27}\) jest równa

A.\( -3 \)

B.\( -\frac{1}{3} \)

C.\( \frac{1}{3} \)

D.\( 3 \)

Wyrażenie \(\Bigl ||x| + 1\Bigl |\) dla \(x \lt 0\) jest równe

A.\( x+1 \)

B.\( x-1 \)

C.\( -x+1 \)

D.\( -x-1 \)

W pewnym sklepie ceny wszystkich płyt CD obniżono o \(20\%\). Zatem za dwie płyty kupione w tym sklepie należy zapłacić mniej o

A.\( 10\% \)

B.\( 20\% \)

C.\( 30\% \)

D.\( 40\% \)

Wielomian \(4x^2 - 100\) jest równy

A.\( (2x-10)^2 \)

B.\( (2x-10)(2x+10) \)

C.\( 4(x-10)^2 \)

D.\( 4(x-10)(x+10) \)

Równanie \(\frac{x^2+36}{x-6}=0\)

A.nie ma rozwiązań

B.ma dokładnie jedno rozwiązanie

C.ma dokładnie dwa rozwiązania

D.ma dokładnie trzy rozwiązania

Największą liczbą całkowitą spełniającą nierówność \((4 + x)^2 \lt (x - 4)(x + 4)\) jest

A.\( -5 \)

B.\( -4 \)

C.\( -3 \)

D.\( -2 \)

Funkcja \(f(x) = 0{,}5x - 6\)

A.jest malejąca i jej wykres przechodzi przez punkt \((0, 6)\)

B.jest rosnąca i jej wykres przechodzi przez punkt \((0, 6)\)

C.jest malejąca i jej wykres przechodzi przez punkt \((0, -6)\)

D.jest rosnąca i jej wykres przechodzi przez punkt \((0, -6)\)

Liczby \(x_1, x_2\) są rozwiązaniami równania \(4(x + 2)(x - 6) = 0\) . Suma \({x_1}^2 + {x_2}^2\) jest równa

A.\( 16 \)

B.\( 32 \)

C.\( 40 \)

D.\( 48 \)

Na rysunku przedstawiony jest wykres funkcji \(y = f(x)\).

Zbiorem wartości tej funkcji jest

A.\( \langle -4,3 \rangle \)

B.\( \langle -4,-1 \rangle \cup \langle 1,3 \rangle\)

C.\( \langle -4,-1 \rangle \cup ( 1,3 \rangle \)

D.\( \langle -5,6 \rangle \)

W trójkącie prostokątnym dane są kąty ostre: \(\alpha =27^\circ \) i \(\beta =63^\circ \). Wtedy \(\frac{\cos \alpha +\sin \beta }{\cos \alpha }\) równa się

A.\( 1+\sin 63^\circ \)

B.\( \sin 63^\circ \)

C.\( 1 \)

D.\( 2 \)

Ciąg arytmetyczny \((a_n)\) jest określony wzorem \(a_n = -2n + 1\) dla \(n \ge 1\). Różnica tego ciągu jest równa

A.\( -1 \)

B.\( 1 \)

C.\( -2 \)

D.\( 3 \)

W ciągu geometrycznym \((a_n)\) dane są \(a_2=\frac{\sqrt{3}}{2}\) i \(a_3=-\frac{3}{2}\). Wtedy wyraz \(a_1\) jest równy

A.\( -\frac{1}{2} \)

B.\( \frac{1}{2} \)

C.\( -\frac{\sqrt{3}}{2} \)

D.\( \frac{\sqrt{3}}{3} \)

Dane są punkty \(A = (6, 1)\) i \(B = (3, 3)\). Współczynnik kierunkowy prostej \(AB\) jest równy

A.\( -\frac{2}{3} \)

B.\( -\frac{3}{2} \)

C.\( \frac{3}{2} \)

D.\( \frac{2}{3} \)

Pole prostokąta jest równe \(40\). Stosunek długości jego boków jest równy \(2:5\). Dłuższy bok tego prostokąta jest równy

A.\( 10 \)

B.\( 8 \)

C.\( 7 \)

D.\( 6 \)

Dany jest trójkąt prostokątny o przyprostokątnych \(5\) i \(12\). Promień okręgu opisanego na tym trójkącie jest równy

A.\( 12 \)

B.\( 8{,}5 \)

C.\( 6{,}5 \)

D.\( 5 \)

Dane są dwa okręgi o promieniach \(12\) i \(17\). Mniejszy okrąg przechodzi przez środek większego okręgu. Odległość między środkami tych okręgów jest równa

A.\( 5 \)

B.\( 12 \)

C.\( 17 \)

D.\( 29 \)

Stożek powstał w wyniku obrotu trójkąta prostokątnego o przyprostokątnych \(13\) i \(15\) wokół dłuższej przyprostokątnej. Promień podstawy tego stożka jest równy

A.\( 15 \)

B.\( 13 \)

C.\( 7{,}5 \)

D.\( 6{,}5 \)

Dany jest sześcian \(ABCDEFGH\). Siatką ostrosłupa czworokątnego \(ABCDE\) jest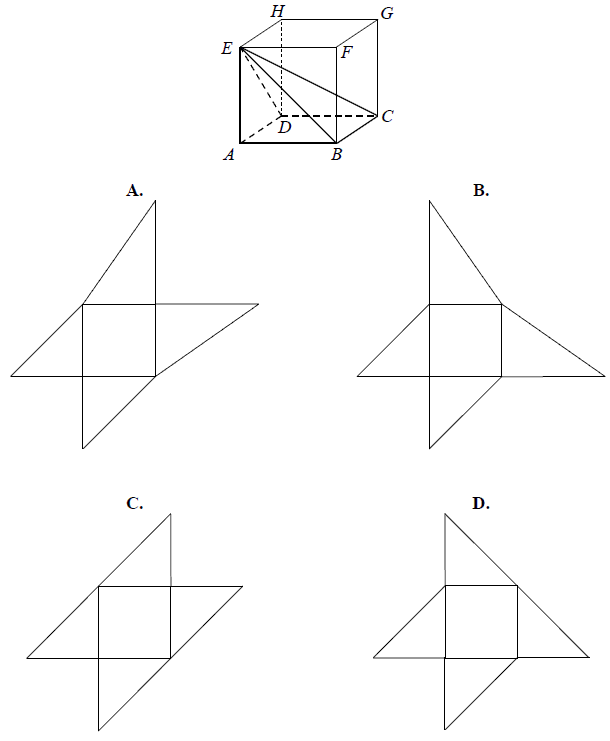

Jeżeli \(A\) jest zdarzeniem losowym oraz \(A'\) jest zdarzeniem przeciwnym do \(A\) i \(P(A)=5\cdot P(A')\), to prawdopodobieństwo zdarzenia \(A\) jest równe

A.\( \frac{4}{5} \)

B.\( \frac{1}{5} \)

C.\( \frac{1}{6} \)

D.\( \frac{5}{6} \)

Rozwiąż nierówność \(-3x^2 + 3x + 36 \ge 0\) .

\(x\in \langle -3; 4 \rangle \)

Funkcja \(f\) jest określona wzorem \(f(x)=\frac{2x-b}{x-9}\) dla \(x \ne 9\). Ponadto wiemy, że \(f(4)=-1\). Oblicz współczynnik \(b\).

\(b=3\)

Podstawy trapezu prostokątnego mają długości \(6\) i \(10\) oraz tangens kąta ostrego jest równy \(3\). Oblicz pole tego trapezu.

\(P=96\)

Trójkąt ABC przedstawiony na poniższym rysunku jest równoboczny, a punkty \(B, C, N\) są współliniowe. Na boku \(AC\) wybrano punkt \(M\) tak, że \(|AM| = |CN|\). Wykaż, że \(|BM| = |MN|\).

Liczby \(64, x, 4\) są odpowiednio pierwszym, drugim i trzecim wyrazem malejącego ciągu geometrycznego. Oblicz piąty wyraz tego ciągu.

\(a_5=\frac{1}{4}\)

Uzasadnij, że dla każdej dodatniej liczby całkowitej n liczba \(3^{n+2} - 2^{n+2} + 3^n - 2^n\) jest wielokrotnością liczby \(10\).

Tabela przedstawia wyniki uzyskane na sprawdzianie przez uczniów klasy III.

Oceny	\(6\)	\(5\)	\(4\)	\(3\)	\(2\)	\(1\)
Liczba uczniów	\(1\)	\(2\)	\(6\)	\(5\)	\(9\)	\(2\)

Oblicz średnią arytmetyczną i kwadrat odchylenia standardowego uzyskanych ocen.

\(\overline{x}=3 \), \(\sigma ^2=1{,}6\)

Rzucamy dwa razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia \(A\) polegającego na tym, że liczba oczek w drugim rzucie jest o \(1\) większa od liczby oczek w pierwszym rzucie.

\(P(A)=\frac{5}{36}\)

Podstawą ostrosłupa \(ABCDS\) jest romb \(ABCD\) o boku długości \(4\). Kąt \(ABC\) rombu ma miarę \(120^\circ \) oraz \(|AS|=|CS|=10\) i \(|BS|=|DS|\). Oblicz sinus kąta nachylenia krawędzi \(BS\) do płaszczyzny podstawy ostrosłupa.

\(\sin \alpha =\sqrt{\frac{22}{23}}\)

Wyznacz równanie okręgu przechodzącego przez punkt \(A = (2, 1)\) i stycznego do obu osi układu współrzędnych. Rozważ wszystkie przypadki.

\((x-1)^2+(y-1)^2=1\) lub \((x-5)^2+(y-5)^2=25\)

Z dwóch miast \(A\) i \(B\), odległych od siebie o \(18\) kilometrów, wyruszyli naprzeciw siebie dwaj turyści. Pierwszy turysta wyszedł z miasta \(A\) o jedną godzinę wcześniej niż drugi z miasta \(B\). Oblicz prędkość, z jaką szedł każdy turysta, jeżeli wiadomo, że po spotkaniu pierwszy turysta szedł do miasta \(B\) jeszcze \(1{,}5\) godziny, drugi zaś szedł jeszcze \(4\) godziny do miasta \(A\).

\(v_1=4\) km/h, \(v_2=3\) km/h