Granica niewłaściwa funkcji
Poziom rozszerzony
Funkcja \(f(x)\) ma granicę niewłaściwą w punkcie \(x_0\) jeżeli \(\lim_{x \to x_0}f(x) = \pm \infty \). Funkcja \(f(x)=\frac{1}{x^2}\) jest określona dla \(x\ne 0\).
W punkcie \(x=0\) nie istnieje wartość funkcji, ale możemy obliczyć granice jednostronne: \[\lim_{x \to 0^-}f(x)=+\infty \] oraz \[\lim_{x \to 0^+}f(x)=+\infty \] Granice jednostronne są równe, zatem w punkcie \(x=0\) mamy granicę niewłaściwą: \[\lim_{x \to 0}f(x)=+\infty \]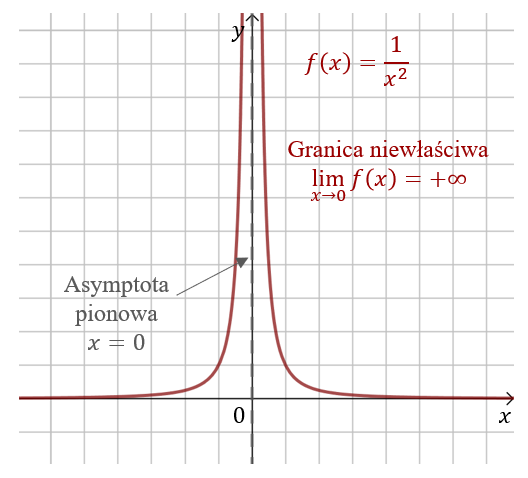
Powiemy, że funkcja zbliżając się do \(x=0\) dąży (ucieka) do plus nieskończoności. Możemy też powiedzieć, że funkcja zbiega do prostej pionowej danej równaniem \(x=0\). Taką prostą pionową nazywamy asymptotą pionową.
W punkcie \(x=0\) nie istnieje wartość funkcji, ale możemy obliczyć granice jednostronne: \[\lim_{x \to 0^-}f(x)=+\infty \] oraz \[\lim_{x \to 0^+}f(x)=+\infty \] Granice jednostronne są równe, zatem w punkcie \(x=0\) mamy granicę niewłaściwą: \[\lim_{x \to 0}f(x)=+\infty \]
Powiemy, że funkcja zbliżając się do \(x=0\) dąży (ucieka) do plus nieskończoności. Możemy też powiedzieć, że funkcja zbiega do prostej pionowej danej równaniem \(x=0\). Taką prostą pionową nazywamy asymptotą pionową. Funkcja \(f(x)=\frac{1}{x-2}+3\) jest określona dla \(x\ne 2\).
W punkcie \(x=2\) możemy zbadać granice jednostronne: \[\lim_{x \to 2^-}f(x)=-\infty \] oraz \[\lim_{x \to 2^+}f(x)=+\infty \] Granice jednostronne w punkcie \(x=2\) są różne, zatem nie istnieje granica funkcji w tym punkcie. Istnieją natomiast granice niewłaściwe jednostronne.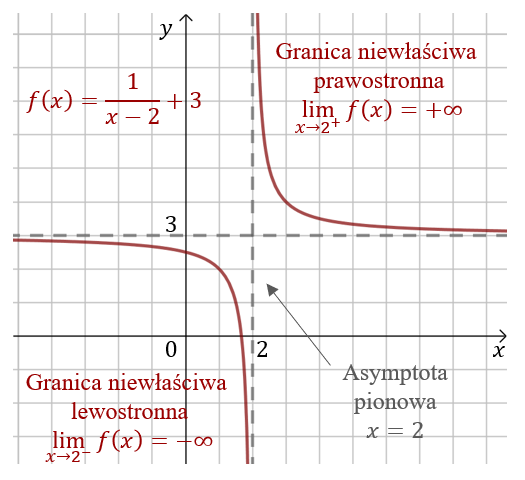
W punkcie \(x=2\) możemy zbadać granice jednostronne: \[\lim_{x \to 2^-}f(x)=-\infty \] oraz \[\lim_{x \to 2^+}f(x)=+\infty \] Granice jednostronne w punkcie \(x=2\) są różne, zatem nie istnieje granica funkcji w tym punkcie. Istnieją natomiast granice niewłaściwe jednostronne.