Funkcja logarytmiczna i jej własności
Poziom podstawowy
Definicja
Funkcję postaci \(f(x)=\log_ax\), gdzie \(a \gt 0\) i \(a\ne 1\), określoną dla \(x\in (0; +\infty )\), nazywamy funkcją logarytmiczną. Wykres funkcji \(f(x) = \log_ax\) zawsze przecina oś \(x\)-ów w punkcie \((1,0)\). 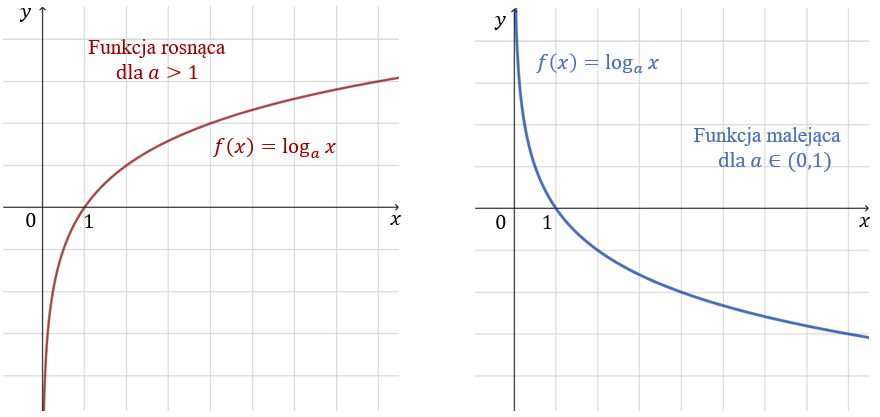
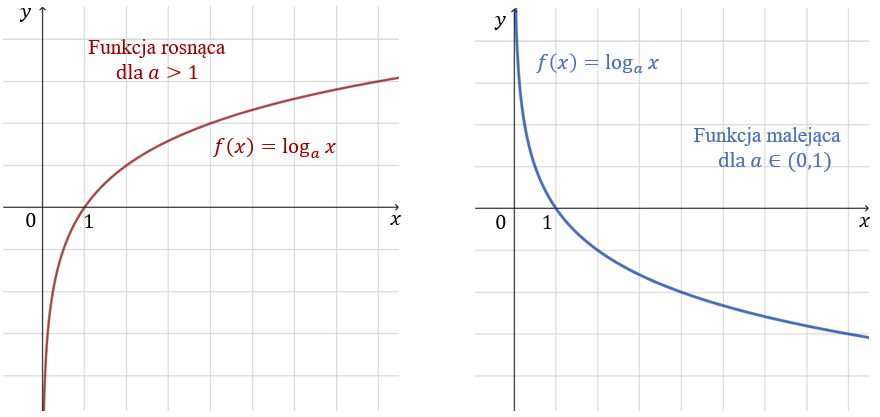
Wykres funkcji \(f(x) = \log_2x\) szkicujemy obliczając wartości funkcji w tabelce:
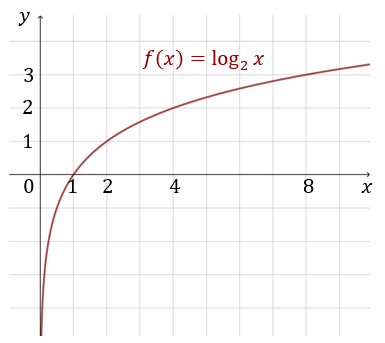 Jest to funkcja rosnąca określona na dziedzinie \(x\in (0, +\infty )\). Zbiorem wartości tej funkcji jest zbiór \(\mathbb{R} \).
Jest to funkcja rosnąca określona na dziedzinie \(x\in (0, +\infty )\). Zbiorem wartości tej funkcji jest zbiór \(\mathbb{R} \).
| \(x\) | \(\frac{1}{2}\) | \(1\) | \(2\) | \(4\) | \(8\) |
| \(y=\log_2x\) | \(-1\) | \(0\) | \(1\) | \(2\) | \(3\) |
 Jest to funkcja rosnąca określona na dziedzinie \(x\in (0, +\infty )\). Zbiorem wartości tej funkcji jest zbiór \(\mathbb{R} \).
Jest to funkcja rosnąca określona na dziedzinie \(x\in (0, +\infty )\). Zbiorem wartości tej funkcji jest zbiór \(\mathbb{R} \). Przykłady kilku różnych funkcji logarytmicznych o podstawie \(a\gt 1\): 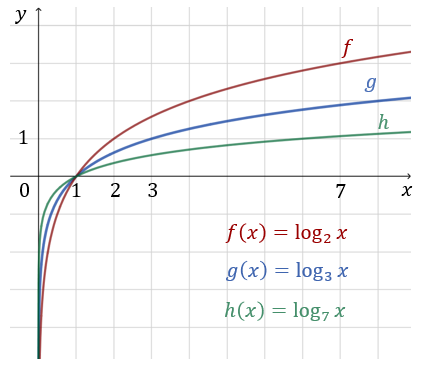

Narysujemy wykres funkcji \(f(x) = \log_{\frac{1}{2}}x\).
Na początek obliczmy wartości tej funkcji dla kilku przykładowych argumentów \(x\). Sporządźmy zatem odpowiednią tabelkę:
i rysujemy wykres: 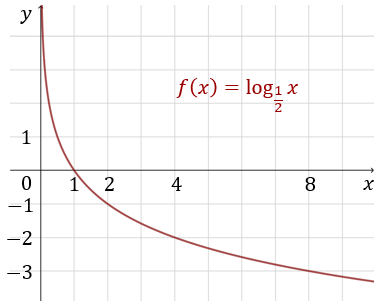 Jest to funkcja malejąca określona na dziedzinie \(x\in (0, +\infty )\). Zbiorem wartości tej funkcji jest zbiór \(\mathbb{R} \).
Jest to funkcja malejąca określona na dziedzinie \(x\in (0, +\infty )\). Zbiorem wartości tej funkcji jest zbiór \(\mathbb{R} \).
Na początek obliczmy wartości tej funkcji dla kilku przykładowych argumentów \(x\). Sporządźmy zatem odpowiednią tabelkę:
| \(x\) | \(\frac{1}{2}\) | \(1\) | \(2\) | \(4\) | \(8\) |
| \(y=\log_{\frac{1}{2}}x\) | \(1\) | \(0\) | \(-1\) | \(-2\) | \(-3\) |
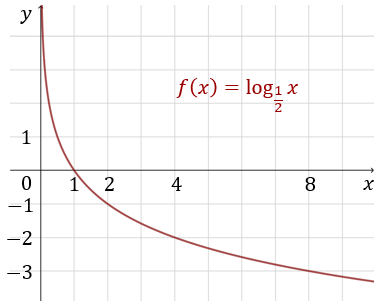 Jest to funkcja malejąca określona na dziedzinie \(x\in (0, +\infty )\). Zbiorem wartości tej funkcji jest zbiór \(\mathbb{R} \).
Jest to funkcja malejąca określona na dziedzinie \(x\in (0, +\infty )\). Zbiorem wartości tej funkcji jest zbiór \(\mathbb{R} \). Przykłady kilku różnych funkcji logarytmicznych o podstawie \(a \lt 1\): 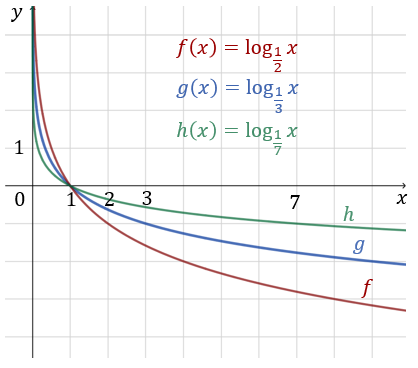

Własności funkcji logarytmicznej \(f(x)=\log_ax\)
- Dziedzina: \(\mathbb{R}^+ \).
- Zbiór wartości: \(\mathbb{R}\).
- Dla \(a\gt 1\) funkcja jest rosnąca, a dla \(a\in (0,1)\) malejąca.
- Funkcja jest różnowartościowa.
- Miejsca zerowe: \(x = 1\).
- Funkcja nie jest parzysta i nie jest nieparzysta.<
Do wykresu funkcji \(f(x)=\log_4x\) nie należy punkt:
A.\( (1,0) \)
B.\( \left ( \frac{1}{2}, -\frac{1}{2} \right ) \)
C.\( (2,2) \)
D.\( (16,2) \)
Narysuj wykres funkcji \(f(x)=\log_5x\) oraz:
oblicz jej wartość dla argumentu \(\sqrt[5]{5\sqrt{125}}\),
znajdź argument dla którego funkcja przyjmuje wartość \(\frac{2}{3}\).
Tematy nadrzędne i sąsiednie