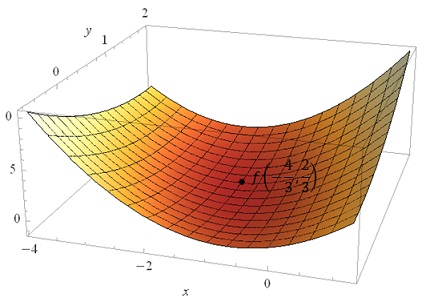
Ekstrema lokalne funkcji dwóch zmiennych - przykład 3

Wyznacz ekstrema lokalne funkcji: \[f(x,y)=x^2+xy+2x+y^2\] Rozwiązanie:

• Liczymy pochodne cząstkowe pierwszego rzędu: \[\begin{split} f'_{x}&=2x+y+2\\f'_{y}&=x+2y \end{split}\]
• Przyrównujemy te pochodne do zera, tworząc układ równań: \[\begin{cases}2x+y+2=0\\x+2y=0\end{cases} \]
• Rozwiązujemy powyższy układ i wyliczamy punkty stacjonarne: \[\begin{split} &\begin{cases}2x+y+2=0\\x+2y=0\end{cases} \\[12pt]&\begin{cases}x=-2y\\y+2(-2y)+2=0\end{cases} \\[12pt]&\begin{cases}x=-2y\\3y=2\end{cases} \\[12pt]&\begin{cases}x=-\frac{4}{3}\\y=\frac{2}{3}\end{cases} \\[12pt] \end{split}\]
• Mamy tylko jeden punkt stacjonarny: \[P=\left ( -\frac{4}{3}, \frac{2}{3} \right )\]
• Liczymy pochodne cząstkowe drugiego rzędu.
  Korzystamy z wyliczonych pochodnych pierwszego rzędu: \[\begin{split} f'_{x}&=2x+y+2\\f'_{y}&=x+2y \end{split}\] Zatem: \[\begin{split} f''_{xx}&=2\\f''_{xy}&=1\\f''_{yx}&=1\\f''_{yy}&=2 \end{split}\]
• Z otrzymanych pochodnych tworzymy wyznacznik: \[W(x,y)=\begin{vmatrix}2&1\\1&2\end{vmatrix} \]
• Obliczamy powyższy wyznacznik dla wyliczonego punktu stacjonarnego (tak naprawdę nie musimy tutaj pamiętać współrzędnych naszego punktu stacjonarnego, bo wyznacznik i tak już tworzą same liczby): \[W(P)=W\left ( -\frac{4}{3}, \frac{2}{3} \right )=\begin{vmatrix}2&1\\1&2\end{vmatrix} =4-1=3\]
• Wyznacznik dla punktu \(P\) wyszedł dodatni, zatem mamy w tym punkcie ekstremum.
• Sprawdzamy jakie ekstremum jest przyjmowane w punkcie \(P\) i w tym celu patrzymy na drugą pochodną po \(x\)-ach:
  \(f''_{x}=2>0\) zatem w punkcie \(P=\left ( -\frac{4}{3}, \frac{2}{3} \right )\) funkcja osiąga minimum.
  Obliczamy wartość minimum: \[f\left ( -\frac{4}{3}, \frac{2}{3} \right )=\left ( -\frac{4}{3} \right )^2+\left ( -\frac{4}{3} \right )\cdot \frac{2}{3}+2\cdot \left ( -\frac{4}{3} \right )+\left ( \frac{2}{3} \right )^2=-\frac{4}{3}\]

Wykres płaszczyzny opisanej przez funkcję \(f(x,y)=x^2+xy+2x+y^2\) wygląda następująco: