Ekstrema lokalne funkcji dwóch zmiennych - przykład 1

Drukuj

Poziom studiów

Wyznacz ekstrema lokalne funkcji: \[f(x,y)=3x^4-\frac{2}{3}y^3+2x^2y-2x^2+y^2\] Rozwiązanie:

Liczymy pochodne cząstkowe pierwszego rzędu: \[\begin{split} f'_{x}&=12x^3+4xy-4x\\f'_{y}&=-2y^2+2x^2+2y \end{split}\]
Przyrównujemy te pochodne do zera, tworząc układ równań: \[\begin{cases}12x^3+4xy-4x=0\\[6pt]-2y^2+2x^2+2y=0\end{cases} \]
Rozwiązujemy powyższy układ równań: \[\begin{split} &\begin{cases}12x^3+4xy-4x=0 \qquad //:4\\-2y^2+2x^2+2y=0 \qquad //:(-2)\end{cases} \\[5pt] \\&\begin{cases}3x^3+xy-x=0\\y^2-x^2-y=0\end{cases} \end{split}\] Rozwiązujemy pierwsze równanie: \[\begin{split} 3x^3+xy-x&=0\\[6pt]x(3x^2+y-1)&=0\\[6pt]x=0\quad &\lor\quad 3x^2+y-1=0\\[6pt]&\lor\quad y=-3x^2+1 \end{split}\] Zatem mamy do rozwiązania dwa układy: \[\begin{cases}x=0\\y^2-x^2-y=0\end{cases} \qquad \text{oraz}\qquad \begin{cases}y=-3x^2+1\\y^2-x^2-y=0\end{cases}\] Rozwiążemy na początku pierwszy układ: \[\begin{split} &\begin{cases}x=0\\[6pt]y^2-x^2-y=0\end{cases}\\[6pt]&\begin{cases}x=0\\[6pt]y^2-y=0\end{cases}\\[6pt]&\begin{cases}x=0\\y(y-1)=0\end{cases}\\[6pt]&\begin{cases}x=0\\[6pt]y=0\end{cases}\qquad \text{lub}\qquad \begin{cases}x=0\\[6pt]y=1\end{cases} \end{split}\] Teraz rozwiążemy drugi układ równań: \[\begin{cases}y=-3x^2+1\\[6pt]y^2-x^2-y=0\end{cases}\\[12pt]\begin{cases}\frac{y-1}{3}=-x^2\\[6pt]y^2-x^2-y=0\end{cases}\] Podstawiamy w drugim równaniu pod \(-x^2\) wyliczone wyrażenie z pierwszego równania: \[\begin{split} y^2+\frac{y-1}{3}-y&=0\qquad //\cdot 3\\[6pt]3y^2+y-1-3y&=0\\[6pt]3y^2-2y-1&=0\\[6pt]\Delta &=4+12=16\\[6pt]y_{1}=\frac{2-4}{6}=-\frac{1}{3}\quad &\lor \quad y_{2}=\frac{2+4}{6}=1 \end{split}\] Czyli mamy: \[\begin{split} &\begin{cases}\frac{y-1}{3}=-x^2\\[6pt]y=-\frac{1}{3}\end{cases}\qquad &\lor \qquad \begin{cases}\frac{y-1}{3}=-x^2\\y=1\end{cases}\\[16pt]&\begin{cases}\frac{-\frac{1}{3}-1}{3}=-x^2\\[6pt]y=-\frac{1}{3}\end{cases}\qquad &\lor \qquad \begin{cases}\frac{1-1}{3}=-x^2\\[6pt]y=1\end{cases}\\[16pt]&\begin{cases}\frac{4}{9}=x^2\\[6pt]y=-\frac{1}{3}\end{cases}\qquad &\lor \qquad \begin{cases}0=x^2\\[6pt]y=1\end{cases}\\[16pt]\begin{cases}x=\frac{2}{3}\\[6pt]y=-\frac{1}{3}\end{cases}&\quad \lor \quad \begin{cases}x=-\frac{2}{3}\\[6pt]y=-\frac{1}{3}\end{cases}\qquad &\lor \qquad \begin{cases}x=0\\[6pt]y=1\end{cases} \end{split}\] Zatem ostatecznie rozwiązaniami układu równań są punkty: \[\begin{cases}x=0\\y=0\end{cases}\quad \lor \quad \begin{cases}x=0\\y=1\end{cases}\quad \lor \quad \begin{cases}x=\frac{2}{3}\\y=-\frac{1}{3}\end{cases}\quad \lor \quad \begin{cases}x=-\frac{2}{3}\\y=-\frac{1}{3}\end{cases}\]
Wypisujemy punkty stacjonarne \[P_{1}=(0,0),\quad P_{2}=(0,1),\quad P_{3}=\left ( \frac{2}{3},-\frac{1}{3} \right ),\quad P_{4}=\left ( -\frac{2}{3},-\frac{1}{3} \right )\]
Liczymy pochodne cząstkowe drugiego rzędu:
Zaczynamy od przypomnienia sobie obliczonych pochodnych pierwszego rzędu: \[\begin{split} f'_{x}&=12x^3+4xy-4x\\[6pt]f'_{y}&=-2y^2+2x^2+2y \end{split}\] I teraz liczymy drugie pochodne: \[\begin{split} f''_{xx}&=36x^2+4y-4\\[6pt]f''_{xy}&=4x\\[6pt]f''_{yx}&=4x\\[6pt]f''_{yy}&=-4y+2 \end{split}\]
Z otrzymanych pochodnych tworzymy wyznacznik: \[W(x,y)=\begin{vmatrix}36x^2+4y-4 & 4x\\4x & -4y+2\end{vmatrix} \]
Obliczamy powyższy wyznacznik kolejno dla wszystkich punktów stacjonarnych:

\[\begin{split} &W(P_{1})=W(0,0)=\begin{vmatrix}36\cdot 0^2+4\cdot 0-4 & 4\cdot 0\\4\cdot 0 & -4\cdot 0+2\end{vmatrix} =\begin{vmatrix}-4 & 0\\0 & 2\end{vmatrix} =-8-0=-8 \end{split} \]

\[\begin{split} &W(P_{2})=W(0,1)=\begin{vmatrix}36\cdot 0^2+4\cdot 1-4 & 4\cdot 0\\4\cdot 0 & -4\cdot 1+2\end{vmatrix} =\begin{vmatrix}0 & 0\\0 & -2\end{vmatrix} =0-0=0 \end{split} \]

\[\begin{split} W(P_{3})&=W(\frac{2}{3},-\frac{1}{3})=\begin{vmatrix}36\cdot \left ( \frac{2}{3} \right )^2+4\cdot \left ( -\frac{1}{3} \right )-4 & 4\cdot \frac{2}{3}\\4\cdot \frac{2}{3} & -4\cdot \left ( -\frac{1}{3} \right )+2\end{vmatrix} =\begin{vmatrix}\frac{32}{3} & \frac{8}{3}\\\frac{8}{3} & \frac{10}{3}\end{vmatrix} =\\[6pt]&= \frac{320}{9}-\frac{64}{9}=\frac{256}{9} \end{split}\]

\[\begin{split} W(P_{4})&=W(-\frac{2}{3},-\frac{1}{3})=\begin{vmatrix}36\cdot \left ( -\frac{2}{3} \right )^2+4\cdot \left ( -\frac{1}{3} \right )-4 & 4\cdot \left ( -\frac{2}{3} \right )\\4\cdot \left ( -\frac{2}{3} \right ) & -4\cdot \left ( -\frac{1}{3} \right )+2\end{vmatrix} =\begin{vmatrix}\frac{32}{3} & -\frac{8}{3}\\-\frac{8}{3} & \frac{10}{3}\end{vmatrix} =\\[6pt]&= \frac{320}{9}-\frac{64}{9}=\frac{256}{9} \end{split} \]
Sprawdzamy dla każdego punktu stacjonarnego czy istnieje w nim ekstremum:
\(W(P_{1})=-8<0\) zatem w punkcie \(P_{1}\) nie ma ekstremum.
\(W(P_{2})=0\) zatem na razie nie wiemy czy w punkcie \(P_{2}\) jest ekstremum.
\(W(P_{3})=\frac{256}{9}>0\) zatem w punkcie \(P_{3}\) jest ekstremum.
\(W(P_{4})=\frac{256}{9}>0\) zatem w punkcie \(P_{4}\) jest ekstremum.
Sprawdzamy jakie ekstrema przyjmuje funkcja w punktach \(P_{3}\) i \(P_{4}\).

\(f''_{xx}(P_{3})=\frac{32}{3}\) zatem w punkcie \(P_{3}\) funkcja ma minimum.
\(f''_{xx}(P_{4})=\frac{32}{3}\) zatem w punkcie \(P_{4}\) funkcja ma minimum.
Obliczamy teraz te minima, korzystając ze wzoru funkcji \(f(x,y)=3x^4-\frac{2}{3}y^3+2x^2y-2x^2+y^2\).
\[\begin{split} f(P_{3})&=f\left ( \frac{2}{3},-\frac{1}{3} \right )=3\left ( \frac{2}{3} \right )^4-\frac{2}{3}\cdot \left ( -\frac{1}{3} \right )^3+2\left ( \frac{2}{3} \right )^2\cdot \left ( -\frac{1}{3} \right )-2\left ( \frac{2}{3} \right )^2+\left ( -\frac{1}{3} \right )^2=-\frac{37}{81} \end{split}\] \[\begin{split} f(P_{4})&=f\left ( -\frac{2}{3},-\frac{1}{3} \right )=3\left ( -\frac{2}{3} \right )^4-\frac{2}{3}\cdot \left ( -\frac{1}{3} \right )^3+2\left ( -\frac{2}{3} \right )^2\cdot \left ( -\frac{1}{3} \right )-2\left ( -\frac{2}{3} \right )^2+\left ( -\frac{1}{3} \right )^2=-\frac{37}{81} \end{split}\]
Sprawdzamy czy istnieje ekstremum w punkcie \(P_{2}=(0,1)\), w którym wyzerował się wyznacznik.
Przypomnijmy sobie macierz drugich pochodnych dla tego punktu: \[f''(P_{2})=\begin{bmatrix}0 & 0\\0 & -2\end{bmatrix}\] Zbadajmy na początku funkcję jednej zmiennej, ze względu na niewiadomą \(x\), przechodzącą przez punkt \(P_{2}=(0,1)\). Jej wzór to: \[\begin{split} f(x,1)&=3x^4-\frac{2}{3}\cdot 1^3+2x^2\cdot 1-2x^2+1^2\\f(x,1)&=3x^4-\frac{2}{3}+2x^2-2x^2+1\\f(x,1)&=3x^4+\frac{1}{3} \end{split}\] Z powyższego wzoru widać, że funkcja dla \(x=0\) ma minimum równe \(\frac{1}{3}\).
Teraz zbadamy funkcję jednej zmiennej, ze względu na niewiadomą \(y\), przechodzącą przez punkt \(P_{2}=(0,1)\). Jej wzór to: \[\begin{split} f(0,y)&=3\cdot 0^4-\frac{2}{3}y^3+2\cdot 0^2\cdot y-2\cdot 0^2+y^2\\f(0,y)&=-\frac{2}{3}y^3+y^2 \end{split}\] Musimy określić, czy ta funkcja osiąga ekstremum dla \(y=1\). W tym celu nie musimy analizować wzoru tej funkcji, ponieważ widzimy, że druga pochodna w tym punkcie jest ujemna: \[f''_{yy}=-2<0\] (odczytujemy to z macierzy drugich pochodnych)
Ponieważ \(f''_{yy}<0\) zatem funkcja jednej zmiennej osiąga dla \(y=1\) ekstremum maksimum.
Podsumowując:
Funkcja jednej zmiennej \(f(x,1)\) osiąga w punkcie \(x=0\) ekstremum minimum.
Funkcja jednej zmiennej \(f(0,y)\) osiąga w punkcie \(y=1\) ekstremum maksimum.
Zatem funkcja dwóch zmiennych \(f(x,y)\) nie ma ekstremum w punkcie \(P_{2}=(0,1)\) (płaszczyzna ma w nim lokalnie kształt siodła).

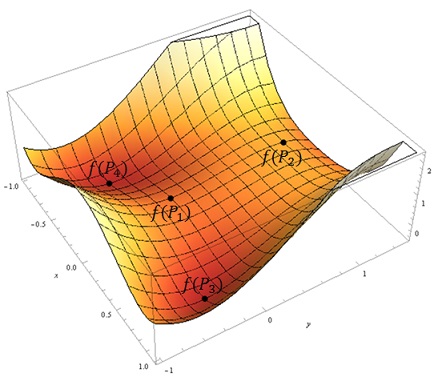Fragment płaszczyzny będącej wykresem funkcji \(f(x,y)\) przedstawiono na poniższym rysunku:

Ten sam wykres nieco obrócony: