Egzamin ósmoklasisty 2023 maj
Szkoła podstawowa
Poniżej przedstawiono składniki potrzebne do przygotowania ciasta na \(8\) gofrów.  Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
 Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe. | Do przygotowania ciasta na \(40\) gofrów, przy zachowaniu właściwych proporcji odpowiednich składników, potrzeba \(10\) jajek. | P | F |
| Do przygotowania ciasta na \(72\) gofry, przy zachowaniu właściwych proporcji odpowiednich składników, potrzeba \(12\) szklanek mleka. | P | F |
Dostęp do pliku jest chroniony hasłem \(∗∗ T ∗∗\) złożonym z dwóch liczb dwucyfrowych oddzielonych literą \(T\). Pierwsza liczba hasła to sześcian liczby \(4\), a druga to najmniejszy wspólny mianownik ułamków \(\frac{1}{15}\) i \(\frac{1}{25}\).
Jakie jest hasło do pliku? Wybierz właściwą odpowiedź spośród podanych.
A.\( 24T45 \)
B.\( 24T75 \)
C.\( 64T45 \)
D.\( 64T75 \)
Dane są cztery wyrażenia: \[G=2x^2+2\qquad H=2x^2+2x\qquad J=2x^2-2\qquad K=2x^2-2x\] Jedno z tych wyrażeń przyjmuje wartość \(0\) dla \(x = 1\) oraz dla \(x = -1\).
Które to wyrażenie? Wybierz właściwą odpowiedź spośród podanych.
A.\( G \)
B.\( H \)
C.\( J \)
D.\( K \)
Marta układała książki na dwóch półkach o tych samych wymiarach wewnętrznych.
Wszystkie książki były jednakowych rozmiarów.
Pierwszą półkę (I) całkowicie wypełniła 12 książkami.
Na drugiej półce (II) postanowiła ustawić książki jedna przy drugiej na całej szerokości półki tak, aby zostało nad nimi wolne miejsce, w sposób pokazany na rysunku.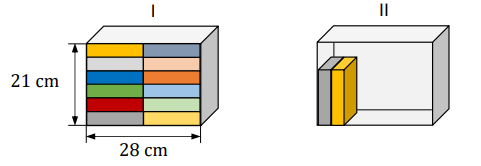
Wszystkie książki były jednakowych rozmiarów.
Pierwszą półkę (I) całkowicie wypełniła 12 książkami.
Na drugiej półce (II) postanowiła ustawić książki jedna przy drugiej na całej szerokości półki tak, aby zostało nad nimi wolne miejsce, w sposób pokazany na rysunku.
Uwaga: na rysunku przedstawiono całkowite wypełnienie książkami pierwszej półki (I) oraz częściowe wypełnienie książkami drugiej półki (II).

Ile najwięcej książek Marta mogła zmieścić na drugiej półce (II) przy wskazanym sposobie ustawienia? Wybierz właściwą odpowiedź spośród podanych.
A.\( 7 \)
B.\( 8 \)
C.\( 10 \)
D.\( 11 \)
Uzupełnij poniższe zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Wyrażenie \(\sqrt{81}-\sqrt{49}\) jest równe A
B
. A.\( 2 \)
B.\( \sqrt{32} \)
C
D
. C.\( 13 \)
D.\( 17 \)
W sadzie rosną drzewa owocowe: grusze i jabłonie. Liczba grusz jest o \(40\%\) większa od liczby jabłoni. Jabłoni jest o \(50\) mniej niż grusz.
Ile jabłoni rośnie w tym sadzie? Wybierz właściwą odpowiedź spośród podanych.
A.\( 20 \)
B.\( 30 \)
C.\( 70 \)
D.\( 125 \)
Uzupełnij poniższe zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Iloraz \(\frac{10^8}{5^8}\) jest równy A
B
. A.\( 5^8 \)
B.\( 2^8 \)
C
D
C.\( 50^9 \)
D.\( 10^6 \)
Liczbę \(x\) powiększono o \(7\), a następnie otrzymany wynik zwiększono 4-krotnie. Liczbę \(y\) zwiększono 5-krotnie, a otrzymany wynik powiększono o \(3\).
Która para wyrażeń algebraicznych poprawnie opisuje wykonane działania? Wybierz właściwą odpowiedź spośród podanych.
A.\( 4(x+7) \) oraz \(5y+3\)
B.\( 4x+7 \) oraz \(5y+3\)
C.\( 4(x+7) \) oraz \(5(y+3)\)
D.\( 4x+7 \) oraz \(5(y+3)\)
Pewien ostrosłup ma \(16\) wierzchołków.
Ile wierzchołków ma graniastosłup o takiej samej podstawie, jaką ma ten ostrosłup? Wybierz właściwą odpowiedź spośród podanych.
A.\( 17 \)
B.\( 30 \)
C.\( 32 \)
D.\( 45 \)
Na planie miasta odległość w linii prostej od punktu oznaczającego przystanek autobusowy Dworzec do punktu oznaczającego przystanek autobusowy Galeria jest równa \(8\) cm. Plan miasta został wykonany w skali \(1 ∶ 4 000\). 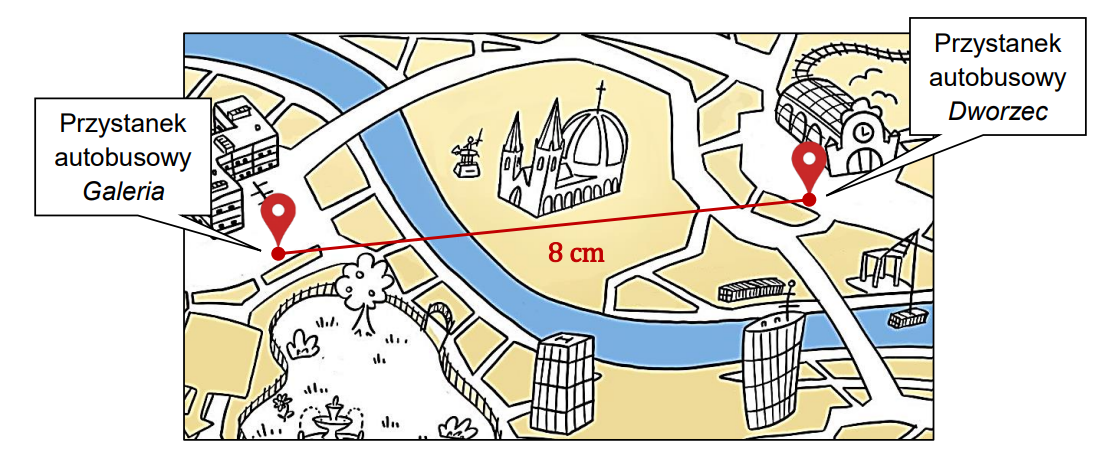

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Odległość w linii prostej w terenie między tymi przystankami jest równa A.\( 320 \) m
B.\( 500 \) m
C.\( 3200 \) m
D.\( 5000 \) m
Z urny, w której jest wyłącznie 18 kul białych i 12 kul czarnych, losujemy 1 kulę.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
| Prawdopodobieństwo wylosowania kuli białej jest równe \(\frac{3}{5}\) | P | F |
| Prawdopodobieństwo wylosowania kuli czarnej jest mniejsze od \(\frac{1}{3}\) | P | F |
W prostokącie \(ABCD\) punkty \(E\) i \(F\) są środkami boków \(BC\) i \(CD\) (zobacz rysunek). Długość odcinka \(EC\) jest równa \(6\) cm, a długość odcinka \(EF\) jest równa \(10\) cm. 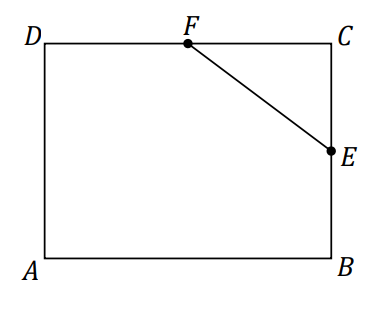

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Obwód prostokąta \(ABCD\) jest równy A.\( 64 \) cm
B.\( 56 \) cm
C.\( 40 \) cm
D.\( 28 \) cm
Agata na dużej kartce w kratkę narysowała figurę złożoną z \(40\) połączonych odcinków, które kolejno ponumerowała liczbami naturalnymi od \(1\) do \(40\).
Na rysunku przedstawiono fragment tej figury, złożony z ośmiu początkowych odcinków. Kolejne odcinki tej figury Agata narysowała według tej samej reguły, którą zastosowała do narysowania odcinków 1-8.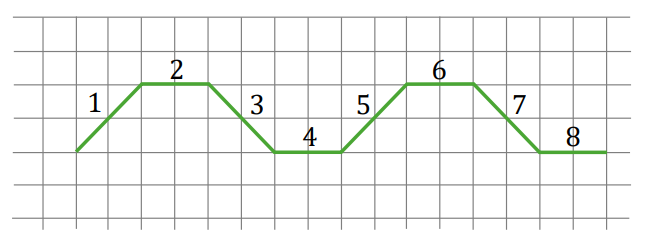
Na rysunku przedstawiono fragment tej figury, złożony z ośmiu początkowych odcinków. Kolejne odcinki tej figury Agata narysowała według tej samej reguły, którą zastosowała do narysowania odcinków 1-8.
Uwaga: wszystkie komórki kratki są takimi samymi kwadratami.

Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F - jeśli jest fałszywe.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe. | Proste zawierające odcinki o numerach \(1\) oraz \(7\) są wzajemnie prostopadłe. | P | F |
| Proste zawierające odcinki o numerach \(5\) oraz \(33\) są wzajemnie równoległe. | P | F |
Na rysunku przedstawiono trzy figury: kwadrat \(F1\), kwadrat F\(\)2 i prostokąt \(F3\), oraz podano ich wymiary. 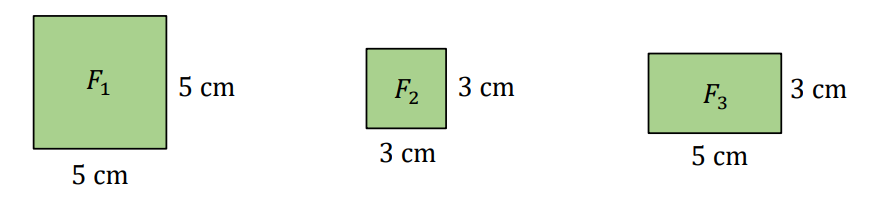


Czy z figur \(F1\), \(F2\), \(F3\) można ułożyć, bez rozcinania tych figur, kwadrat \(K\) o polu \(49\) cm\(^2\)? Wybierz odpowiedź A albo B i jej uzasadnienie spośród 1., 2. albo 3.

W czworokącie \(ABCD\) boki \(AB\), \(CD\) i \(DA\) mają równe długości, a kąt \(BCD\) ma miarę \(131^\circ \). Przekątna \(AC\) dzieli ten czworokąt na trójkąt równoboczny i na trójkąt równoramienny (zobacz rysunek). 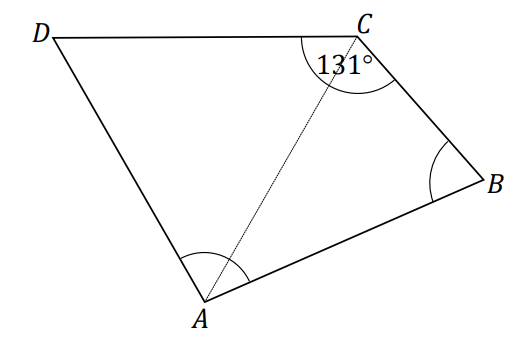 Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
 Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe. | Kąt \(ABC\) ma miarę \(60^\circ \). | P | F |
| Kąt \(DAB\) ma miarę \(98^\circ \). | P | F |
Cena biletu do teatru jest o \(64\) zł większa od ceny biletu do kina. Za \(4\) bilety do teatru i \(5\) biletów do kina zapłacono łącznie \(400\) zł.
Oblicz cenę jednego biletu do teatru. Zapisz obliczenia.
Pociąg przebył ze stałą prędkością drogę \(700\) metrów w czasie \(50\) sekund. Przy zachowaniu tej samej, stałej prędkości ten sam pociąg drogę równą jego długości przebył w czasie \(15\) sekund.
Oblicz długość tego pociągu. Zapisz obliczenia.
W czworokącie \(ABCD\) o polu \(48\) cm\(^2\) przekątna \(AC\) ma długość \(8\) cm i dzieli ten czworokąt na dwa trójkąty: \(ABC\) i \(ACD\) (zobacz rysunek). Wysokość trójkąta \(ACD\) poprowadzona z wierzchołka \(D\) do prostej \(AC\) jest równa \(2\) cm. 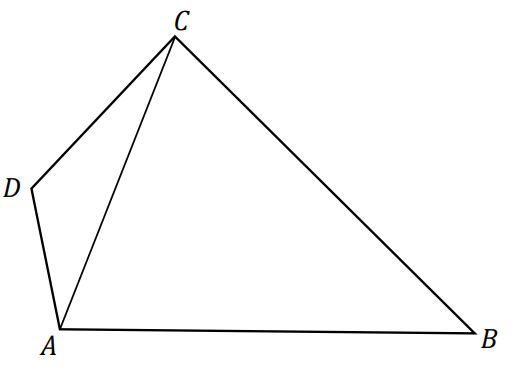 Oblicz wysokość trójkąta \(ABC\) poprowadzoną z wierzchołka \(B\) do prostej \(AC\). Zapisz obliczenia.
Oblicz wysokość trójkąta \(ABC\) poprowadzoną z wierzchołka \(B\) do prostej \(AC\). Zapisz obliczenia.
 Oblicz wysokość trójkąta \(ABC\) poprowadzoną z wierzchołka \(B\) do prostej \(AC\). Zapisz obliczenia.
Oblicz wysokość trójkąta \(ABC\) poprowadzoną z wierzchołka \(B\) do prostej \(AC\). Zapisz obliczenia.Z pięciu prostopadłościennych klocków o jednakowych wymiarach ułożono figurę. Kształt i wybrane wymiary tej figury przedstawiono na rysunku. 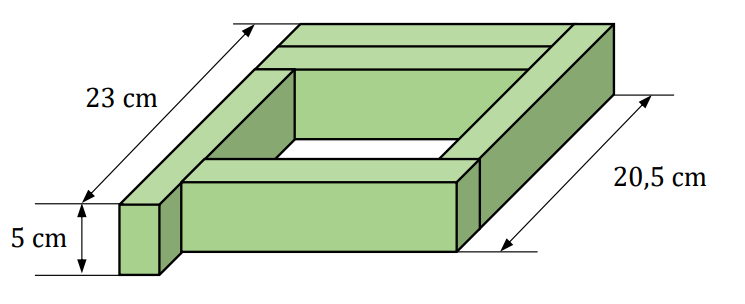

Oblicz objętość jednego klocka. Zapisz obliczenia.
Tematy nadrzędne i sąsiednie