Egzamin ósmoklasisty 2021 maj
Szkoła podstawowa
Rozwiązania zadań z egzaminu ósmoklasisty z 26 maja 2021.Na diagramie słupkowym przedstawiono liczby medali zdobytych na czterech letnich igrzyskach olimpijskich przez reprezentację Polski.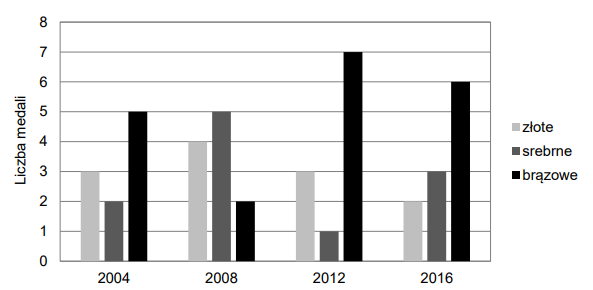 
Oceń prawdziwość podanych zdań, dotyczących medali zdobytych przez reprezentację Polski podczas letnich igrzysk olimpijskich w latach 2004–2016. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
| Liczba zdobytych złotych medali stanowi więcej niż jedną trzecią liczby wszystkich zdobytych medali. | P | F |
| Podczas letnich igrzysk olimpijskich średnio zdobywano \(3\) złote medale. | P | F |
Dane są cztery liczby \(x, y, t, u\) zapisane za pomocą wyrażeń arytmetycznych: \[x=-62{,}5+30\qquad y=-14{,}4-12{,}6\qquad t=-12:0{,}3\qquad u=-8,02\cdot 6\]
Która z tych liczb jest największa? Wybierz właściwą odpowiedź spośród podanych.
A.\( x \)
B.\( y \)
C.\( t \)
D.\( u \)
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Wartość wyrażenia \(\frac{3}{7}+\frac{3}{5}\) jest liczbą A
B
. A.mniejszą od \( 1 \)
B.większą od \( 1 \)
C
D
C.ujemną
D.dodatnią
Z reguł działań na potęgach wynika, że: \[(200\ 000)^3=(2\cdot 100\ 000)^3=(2\cdot 10^5)^3=2^3\cdot 10^{15}\]
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Z tych samych reguł wynika, że liczba \((60\ 000\ 000)^3\) jest równa A.\( 6^3\cdot 10^{21} \)
B.\( 6\cdot 10^{21} \)
C.\( 6^3\cdot 10^{10} \)
D.\( 6\cdot 10^{10} \)
Czy iloczyn dowolnych pięciu kolejnych liczb całkowitych jest podzielny przez \(10\)? Wybierz odpowiedź A albo B i jej uzasadnienie spośród 1., 2. albo 3.
Podatek od dochodów za rok 2016 w Polsce był obliczany według sposobów przedstawionych w poniższej tabeli. 
W 2016 roku podstawa obliczenia podatku dla pani Zofii wyniosła \(97\ 300\) zł. Wysokość podatku (w zł) od dochodu pani Zofii opisuje wyrażenie
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
W 2016 roku podstawa obliczenia podatku dla pana Jana wyniosła \(84\ 500\) zł. Wysokość podatku (w zł) od dochodu pana Jana opisuje wyrażenie A
B
A.\( 0{,}18 \cdot 84\ 500 - 556{,}02 \)
B.\( 0{,}18 \cdot (84\ 500 - 556{,}02)\)
C
D
C.\( 14\ 839{,}02 + 0,32 ּ\cdot 85\ 528 \)
D.\( 14\ 839{,}02 + 0,32 \cdot (97\ 300 - 85\ 528) \)
Do liczby \((-\sqrt{10})\) dodajemy \(5\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Otrzymany wynik jest liczbą A.większą od \(1\).
B.dodatnią mniejszą od \(1\).
C.mniejszą od \((-8)\).
D.ujemną większą od \((-8)\).
Informacje do zadań 8. i 9.
Trójki liczb naturalnych \(a\), \(b\) i \(c\), które spełniają warunek \(a^2+b^2=c^2\), nazywamy trójkami pitagorejskimi. Niektóre z nich znajdujemy z wykorzystaniem wzorów: \[a=2n+1\qquad b=2n(n+1)\qquad c=2n^2+2n+1\] gdzie \(n\) oznacza dowolną liczbę naturalną \((n\ge 1)\). W zadaniach 8. i 9. liczby \(a\), \(b\) i \(c\) są wyznaczone za pomocą tych wzorów. Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Liczba \(a\) zawsze będzie A
B
A.parzysta
B.nieparzysta
C
D
C.\( 1 \)
D.\( n \)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Jeżeli najmniejsza z liczb \(a\), \(b\) i \(c\) jest równa \(9\), to największa z tych liczb jest równa A.\( 41 \)
B.\( 73 \)
C.\( 145 \)
D.\( 181 \)
Ala kupiła trzy zeszyty i blok rysunkowy. Średnia arytmetyczna cen tych czterech artykułów była równa \(6\) zł. Zeszyty kosztowały łącznie \(15\) zł.
Ile kosztował blok rysunkowy? Wybierz właściwą odpowiedź spośród podanych.
A.\( 4 \) zł
B.\( 5 \) zł
C.\( 8 \) zł
D.\( 9 \) zł
W pewnej loterii wśród \(150\) losów co szósty był wygrywający, a pozostałe losy były puste. Wyciągnięto \(30\) losów i żaden z nich nie był wygrywający. Wyciągnięto jeszcze jeden los. Prawdopodobieństwo tego, że będzie to los wygrywający, wynosi
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Na loterię przygotowano A
B
losów wygrywających. A.\( 120 \)
B.\( 25 \)
C
D
C.\( \frac{25}{120} \)
D.\( \frac{25}{125} \)
W trójkącie \(ABC\) narysowano dwie wysokości: \(CD\) i \(AE\), jak na rysunku. Kąt rozwarty pomiędzy tymi wysokościami jest równy \(138^\circ \).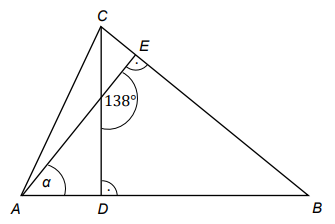 
Jaką miarę ma kąt α zaznaczony na rysunku? Wybierz właściwą odpowiedź spośród podanych.
A.\( 38^\circ \)
B.\( 42^\circ \)
C.\( 45^\circ \)
D.\( 48^\circ \)
Listewkę o długości \(50\) cm planowano pociąć na równe części. Iwona zaproponowała podział na kawałki po \(5\) cm i zaznaczyła na listewce czerwonym kolorem linie cięcia. Agata chciała podzielić tę samą listewkę na części po \(2\) cm i linie cięcia zaznaczyła na zielono.
Ile razy linia czerwona pokrywała się z linią zieloną? Wybierz właściwą odpowiedź spośród podanych.
A.\( 5 \)
B.\( 4 \)
C.\( 3 \)
D.\( 2 \)
Skrzynia ma kształt prostopadłościanu. Podłoga skrzyni ma wymiary \(1{,}5\) m i \(1{,}2\) m, a wysokość skrzyni jest równa \(1\) m. Piasek wsypany do skrzyni zajmuje \(\frac{3}{4}\) jej pojemności.
Ile metrów sześciennych piasku wsypano do skrzyni? Wybierz właściwą odpowiedź spośród podanych.
A.\( 1{,}8\ \text{m}^3\)
B.\( 0{,}45\ \text{m}^3\)
C.\( 1{,}35\ \text{m}^3\)
D.\( 2{,}4\ \text{m}^3\)
Staś ma dwa jednakowe klocki w kształcie ostrosłupa prawidłowego czworokątnego, każdy o polu powierzchni całkowitej \(80\ \text{cm}^2\). Podstawa i ściana boczna klocka mają równe pola. Staś skleił oba klocki podstawami tak, jak na rysunku.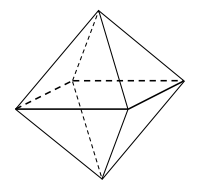 
Jakie pole powierzchni ma bryła otrzymana przez Stasia? Wybierz właściwą odpowiedź spośród podanych.
A.\( 112\ \text{cm}^2 \)
B.\( 128\ \text{cm}^2 \)
C.\( 144\ \text{cm}^2 \)
D.\( 160\ \text{cm}^2 \)
Paweł powiedział, że podzieli tabliczkę czekolady w taki sposób, że bratu przypadnie \(\frac{1}{2}\) całej tabliczki, siostrze \(\frac{5}{12}\) całej tabliczki, a jemu \(\frac{1}{6}\) całej tabliczki. Czy taki podział tabliczki czekolady jest możliwy? Uzasadnij swoją odpowiedź.
Adam mieszka w miejscowości Bocianowo, a jego kolega Bartek – w miejscowości Żabno. Adam umówił się z Bartkiem w Żabnie na godzinę 18:00. Wyjechał z Bocianowa na skuterze o godzinie 17:20. Średnia prędkość jazdy Adama była równa \(25 \frac{\text{km}}{\text{h}}\). Na kwadratowej siatce Adam przedstawił schemat trasy, którą jechał. O której godzinie Adam dotarł na spotkanie z Bartkiem? Zapisz obliczenia.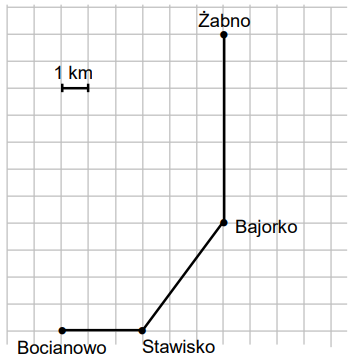 
Ania chciała kupić \(10\) jednakowych puszek karmy dla psa, ale zabrakło jej \(11\) złotych. Kupiła \(6\) takich puszek karmy i zostało jej \(3{,}40\) złotych. Ile kosztuje jedna puszka karmy? Zapisz obliczenia.
Dany jest prostokąt \(ABCD\) o wymiarach \(12\) cm i \(16\) cm. Odcinek \(AC\) jest przekątną tego prostokąta. Odcinek \(DS\) jest wysokością trójkąta \(ACD\) (patrz rysunek).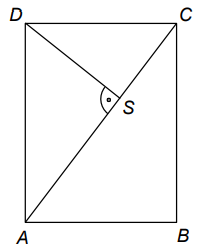 
Oblicz długość odcinka \(DS\). Zapisz obliczenia.
Oblicz długość odcinka \(DS\). Zapisz obliczenia.Tematy nadrzędne i sąsiednie