Funkcje trygonometryczne kąta ostrego
Poziom podstawowy
Rozważmy trójkąt prostokątny o przyprostokątnych \(a\) i \(b\) oraz przeciwprostokątnej \(c\). Zaznaczmy w tym trójkącie jeden kąt ostry \(\alpha\):  Wówczas mamy następujące definicje funkcji trygonometrycznych: \[\begin{split} &\\&\sin{\alpha }=\frac{a}{c}\qquad \qquad &\cos{\alpha }=\frac{b}{c}\\[10pt]&\text{tg}{\alpha }=\frac{a}{b}\qquad \qquad &\text{ctg}{\alpha }=\frac{b}{a} \end{split}\] Pisząc słowami: \[\begin{split} &\sin{\alpha }=\frac{\text{przyprostokątna naprzeciwko kąta}\ \alpha }{\text{przeciwprostokątna}}\\[14pt]&\cos{\alpha }=\frac{\text{przyprostokątna przy kącie}\ \alpha }{\text{przeciwprostokątna}}\\[14pt]&\text{tg}{\alpha }=\frac{\text{przyprostokątna naprzeciwko kąta}\ \alpha }{\text{przyprostokątna przy kącie}\ \alpha }\\[14pt]&\text{ctg}{\alpha }=\frac{\text{przyprostokątna przy kącie}\ \alpha }{\text{przyprostokątna naprzeciwko kąta}\ \alpha } \end{split}\]
Wówczas mamy następujące definicje funkcji trygonometrycznych: \[\begin{split} &\\&\sin{\alpha }=\frac{a}{c}\qquad \qquad &\cos{\alpha }=\frac{b}{c}\\[10pt]&\text{tg}{\alpha }=\frac{a}{b}\qquad \qquad &\text{ctg}{\alpha }=\frac{b}{a} \end{split}\] Pisząc słowami: \[\begin{split} &\sin{\alpha }=\frac{\text{przyprostokątna naprzeciwko kąta}\ \alpha }{\text{przeciwprostokątna}}\\[14pt]&\cos{\alpha }=\frac{\text{przyprostokątna przy kącie}\ \alpha }{\text{przeciwprostokątna}}\\[14pt]&\text{tg}{\alpha }=\frac{\text{przyprostokątna naprzeciwko kąta}\ \alpha }{\text{przyprostokątna przy kącie}\ \alpha }\\[14pt]&\text{ctg}{\alpha }=\frac{\text{przyprostokątna przy kącie}\ \alpha }{\text{przyprostokątna naprzeciwko kąta}\ \alpha } \end{split}\] Graficzna metoda zapamiętania
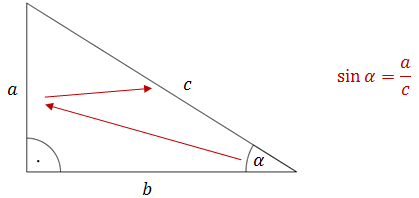
Aby obliczyć sinus kąta ostrego w trójkącie prostokątnym, to:- patrzymy najpierw na przyprostokątną naprzeciwko kąta,
- potem na przeciwprostokątną.
 Aby obliczyć cosinus kąta ostrego w trójkącie prostokątnym, to:
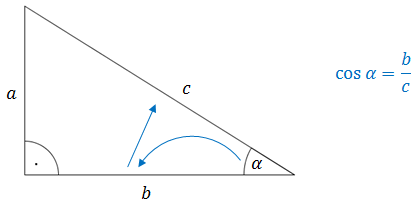
Aby obliczyć cosinus kąta ostrego w trójkącie prostokątnym, to: - patrzymy najpierw na przyprostokątną przy kącie,
- potem na przeciwprostokątną.
 Aby obliczyć tangens kąta ostrego w trójkącie prostokątnym, to:
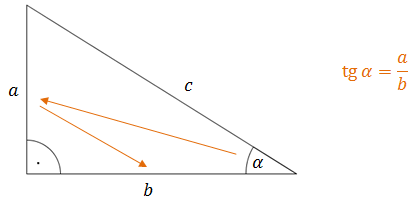
Aby obliczyć tangens kąta ostrego w trójkącie prostokątnym, to: - patrzymy najpierw na przyprostokątną naprzeciwko kąta,
- potem na drugą przyprostokątną.
 Aby obliczyć cotangens kąta ostrego w trójkącie prostokątnym, to:
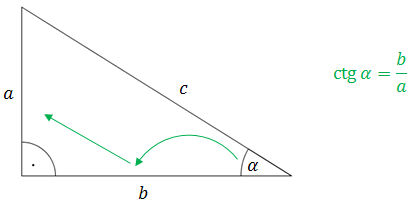
Aby obliczyć cotangens kąta ostrego w trójkącie prostokątnym, to: - patrzymy najpierw na przyprostokątną przy kącie,
- potem na drugą przyprostokątną.
Podaj wartości wszystkich funkcji trygonometrycznych dla zaznaczonego kąta \(\alpha \). ![[obrazek dla przykładu 1]](grafika/g0032.png)
![[obrazek dla przykładu 1]](grafika/g0032.png)
Bezpośrednio z rysunku odczytujemy, że: \[\begin{split} &\\&\sin{\alpha }=\frac{4}{5}\qquad \qquad &\cos{\alpha }=\frac{3}{5}\\[10pt]&\text{tg}{\alpha }=\frac{4}{3}\qquad \qquad &\text{ctg}{\alpha }=\frac{3}{4} \end{split}\]
Podaj wartości wszystkich funkcji trygonometrycznych dla zaznaczonego kąta \(\beta\). ![[obrazek dla przykładu 21]](grafika/g0033.png)
![[obrazek dla przykładu 21]](grafika/g0033.png)
Z danego rysunku odczytujemy, że: \[\begin{split} &\\&\sin{\beta}=\frac{3}{5}\qquad \qquad &\cos{\beta}=\frac{4}{5}\\[10pt]&\text{tg}{\beta}=\frac{3}{4}\qquad \qquad &\text{ctg}{\beta}=\frac{4}{3} \end{split}\]
Podaj wartości funkcji trygonometrycznych dla kąta \(\alpha \) zaznaczonego na rysunku. 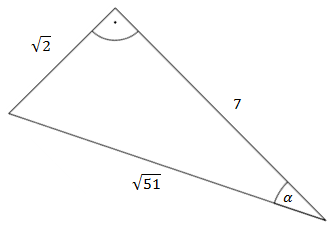

Bezpośrednio z rysunku odczytujemy, że: \[\begin{split} &\\&\sin{\alpha }=\frac{\sqrt{2}}{\sqrt{51}}\qquad \qquad &\cos{\alpha }=\frac{7}{\sqrt{51}}\\[10pt]&\text{tg}{\alpha }=\frac{\sqrt{2}}{7}\qquad \qquad &\text{ctg}{\alpha }=\frac{7}{\sqrt{2}} \end{split}\]
Oblicz wartości funkcji trygonometrycznych dla kąta \(\alpha \) zaznaczonego na rysunku. 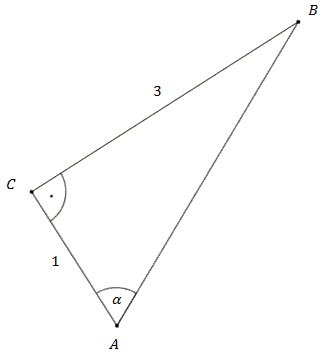

Na początku musimy obliczyć długość przeciwprostokątnej \(AB\). Korzystamy z twierdzenia Pitagorasa: \[\begin{split} |AB|^2&=1^2+3^2\\|AB|^2&=1+9\\|AB|^2&=10\\|AB|&=\sqrt{10} \end{split}\] Zatem: \[\begin{split} &\\&\sin{\alpha }=\frac{3}{\sqrt{10}}\qquad \qquad &\cos{\alpha }=\frac{1}{\sqrt{10}}\\[10pt]&\text{tg}{\alpha }=\frac{3}{1}\qquad \qquad &\text{ctg}{\alpha }=\frac{1}{3} \end{split}\]
Tematy nadrzędne i sąsiednie