Area of a Triangle
To find the area of a triangle, multiply the base by the height, and then divide by \(2\).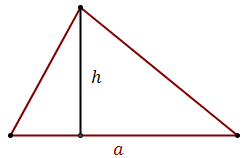 \[ A = \frac{1}{2}ah\] The division by \(2\) comes from the fact that a parallelogram can be divided into \(2\) triangles, like in the diagram bellow:
\[ A = \frac{1}{2}ah\] The division by \(2\) comes from the fact that a parallelogram can be divided into \(2\) triangles, like in the diagram bellow: 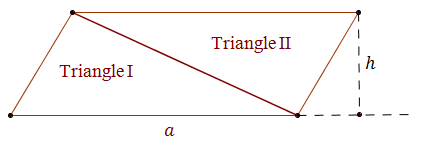 To find the area of a triangle we can use some more formulaes:
To find the area of a triangle we can use some more formulaes: | Formula | Diagram |
| \[ A = \frac{1}{2}ah\] | ![[obrazek]](grafika/g0090.png) |
| \[A=\frac{1}{2}ab\sin \gamma \] | ![[obrazek]](grafika/g0091.png) |
| \[ A=\sqrt{p(p-a)(p-b)(p-c)} \] where: \(p=\frac{a+b+c}{2}\) | ![[obrazek]](grafika/g0092.png) |
| \[ A=\frac{abc}{4R} \] | ![[obrazek]](grafika/g0093.png) |
| \[ A=2R^2\sin \alpha \sin \beta \sin \gamma \] | ![[obrazek]](grafika/g0094.png) |
| \[ A=rp \] where: \(p=\frac{a+b+c}{2}\) | ![[obrazek]](grafika/g0095.png) |
Next topic
Derivatives