Jesteś tutaj: Matura → Zadania maturalne CKE - poziom rozszerzony
Zadania maturalne CKE - poziom rozszerzony
Oblicz wartość wyrażenia \[\log_83^{3\log_32-\log_{27}8-\log_94}\] Zapisz obliczenia.
Liczby \(a\), \(b\), \(c\) są kolejnymi wyrazami ciągu arytmetycznego o różnicy równej \(7\). Jedna z tych liczb jest wielokrotnością liczby \(7\).
Wykaż, że iloczyn \(a\cdot b\cdot c\) jest podzielny przez \(294\).
Niech \(a\), \(b\) będą liczbami całkowitymi, dla których zachodzi równość \(2a^2+a=3b^2+b\).
Wykaż, że jeśli \(5\) jest dzielnikiem liczby \(a-b\), to \(25\) również jest dzielnikiem liczby \(a-b\).
Rozpatrzmy liczby naturalne większe od \(1000\), w których zapisie występuje tylko cyfra 1: \[a=\underbrace{11...111}_{n}\]
Wykaż, że jeśli liczba \(a\) zapisana za pomocą \(n\) jedynek jest liczbą pierwszą, to liczba \(n\) również jest liczbą pierwszą.
Suma liczb całkowitych \(x\) i \(y\) jest podzielna przez \(3\).
Wykaż, że suma sześcianów liczb \(x\) i \(y\) jest podzielna przez \(9\).
W rozwinięciu wyrażenia \((a + b)^n\) dla pewnego \(n \in \mathbb{N} \) suma współczynników przy wyrazach \(a^{n-2}b^2\) oraz \(a^{n-1}b\) jest równa \(66\).
Oblicz \(n\). Zapisz obliczenia.
Niech \(a\), \(b\), \(c\) będą takimi liczbami całkowitymi, że \(a\sqrt{2}+b\sqrt{3}+c\sqrt{6}=0\).
Wykaż, że \(a=b=c=0\).
Wykaż, że liczba \(a=(\sqrt{5}+2)^{2022}+(\sqrt{5}-2)^{2022}\) jest wymierna.
Rozwiąż nierówność \(2x^2+x|2x-1|\le3\).
Zapisz obliczenia.
Zapisz obliczenia.
Rozwiąż nierówność \[x+4+\frac{8}{x-4}\ge\frac{-2x-8}{x^2-16}\] Zapisz obliczenia.
Wyznacz wszystkie wartości parametru \(m\), dla których równanie \[2x^2-(2m+7)x+m^2-3m+21=0\] ma dwa różne rozwiązania rzeczywiste \(x_1\) oraz \(x_2\), spełniające warunek \(x_1=2x_2\). Zapisz obliczenia.
Wykaż, że dla każdej liczby naturalnej \(n\) prawdziwe są nierówności \[2(\sqrt{n+2}-\sqrt{n+1})\lt\frac{1}{\sqrt{n+1}}\quad \text{i}\quad \frac{1}{\sqrt{n+1}}\lt2(\sqrt{n+1}-\sqrt{n})\]
Rozwiąż układ równań \[\begin{cases} x^2-2x+y^2=24 \\ x^2-10x+y^2-8y+40=0 \end{cases}\] Zapisz obliczenia.
Dane są funkcje \(k\) oraz \(p\). Funkcja \(k\) jest określona wzorem \(k(x) = 5 - x^2\) dla każdej liczby rzeczywistej \(x\). Funkcja \(p\) jest określona wzorem \(p(x) =\sqrt{1-x}\) dla każdej liczby rzeczywistej \(x\) nie większej od \(1\). Funkcje \(f\) oraz \(g\) są określone następująco:
\(f=k\circ p\) oraz \(g=p\circ k\)
Wyznacz wzory i dziedziny funkcji \(f\) oraz \(g\).
Narysuj wykres funkcji \(f(x)=\frac{|x^2-9|}{3-x}\).
Wyznacz wszystkie wartości parametru \(m\), dla których równanie \(f(x)=m\) nie ma rozwiązania. Zapisz obliczenia.
Dany jest rosnący ciąg arytmetyczny \((a_n)\) określony dla każdej liczby naturalnej \(n \ge 1\). Ciąg \((a_1\cdot a_2,\ a_2\cdot a_3,\ a_3\cdot a_1, )\) jest geometryczny i ma wyrazy różne od zera.
Oblicz iloraz tego ciągu geometrycznego. Zapisz obliczenia.
Na płaszczyźnie, w kartezjańskim układzie współrzędnych \((x, y)\), dane są dwie proste \(l_1\) oraz \(l_2\). Kąt między tymi prostymi ma miarę \(45^\circ\). Współczynnik kierunkowy w równaniu prostej \(l_1\) jest równy \(\frac{2}{3}\).
Oblicz współczynnik kierunkowy w równaniu prostej \(l_2\). Zapisz obliczenia.
Rozwiąż równanie \[\cos^2x-\frac{2\sqrt{3}}{3}\sin x\cos x-\sin^2x=0\] w przedziale \([-\pi,\pi]\). Zapisz obliczenia.
Na szczycie wieży o wysokości \(h\) umieszczono pionowo antenę radiową stacji nadawczej o długości \(l\) (\(l\gt h\)). Punkt \(O\) leży na płaszczyźnie poziomej przechodzącej przez podnóże wieży, a punkt \(A\) znajduje się na końcu anteny. Koniec anteny \(A\) widać z punktu \(O\) pod dwukrotnie większym kątem niż wieżę (zobacz rysunek). 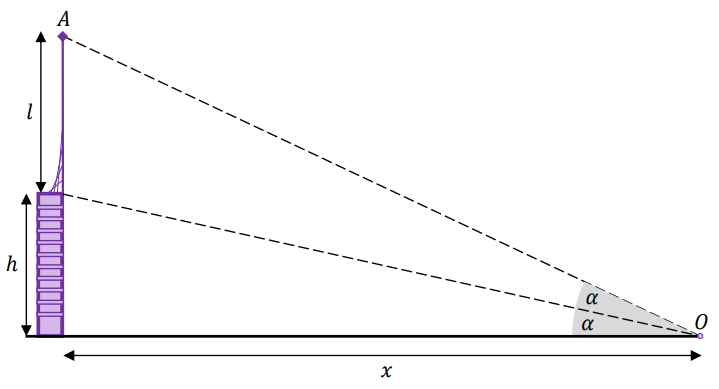

Oblicz odległość \(x\) podnóża wieży od punktu \(O\). Zapisz obliczenia.
W pewien okrąg wpisano czworokąt \(ABCD\) taki, że \(|AB| = 10\), \(|CD| = 6\) oraz \(|BC| = |BD|\). Styczna do tego okręgu w punkcie \(C\) tworzy z bokiem \(CD\) kąt \(\alpha\) o mierze \(30^\circ\) (zobacz rysunek). 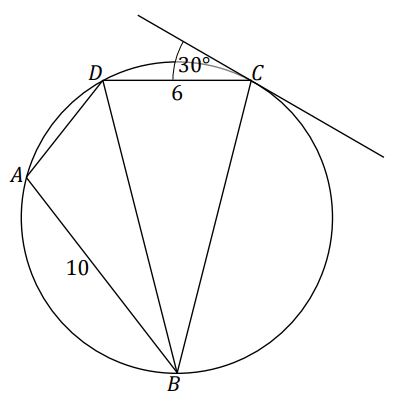

Oblicz pole czworokąta \(ABCD\). Zapisz obliczenia.
W trapezie \(ABCD\) przekątna \(BD\) jest dwusieczną kąta \(CBA\) i przecina przekątną \(AC\) w punkcie \(K\), takim, że \(|CK|:|KA| = 1 : 3\). Pole tego trapezu jest równe \(100(\sqrt{6}-\sqrt{2})\), \(\sin\sphericalangle BAD=\frac{\sqrt{6}+\sqrt{2}}{4}\), \(|AD| = 10\) oraz kąt \(BAD\) jest ostry.
Oblicz długości pozostałych boków trapezu \(ABCD\). Zapisz obliczenia.
Punkt \(D\) leży wewnątrz trójkąta \(ABC\). Prosta przechodząca przez punkt \(D\) i równoległa do boku \(AC\) przecina bok \(AB\) w punkcie \(K\), a bok \(BC\) w punkcie \(L\). Prosta przechodząca przez punkt \(D\) i równoległa do boku \(BC\) przecina bok \(AB\) w punkcie \(M\), a bok \(AC\) w punkcie \(N\) (zobacz rysunek). Stosunek obwodu trójkąta \(KMD\) do obwodu trójkąta \(KBL\) jest równy \(5 : 7\), a stosunek obwodu trójkąta \(KMD\) do obwodu trójkąta \(AMN\) jest równy \(5 : 8\). Pole czworokąta \(DLCN\) jest równe \(15\). 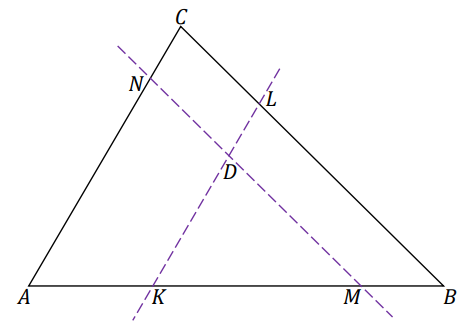

Oblicz pole trójkąta \(ABC\). Zapisz obliczenia.
Funkcja \(f\) jest określona wzorem \[f(x)=\frac{\sqrt{2x}}{5+x^2}-3^{-x-1}\] dla każdej nieujemnej liczby rzeczywistej \(x\).
Wykaż, że funkcja \(f\) ma co najmniej jedno miejsce zerowe dodatnie mniejsze od \(3\).
Funkcja \(f\) jest określona wzorem \(f(x)=\sqrt{1+4x}\) dla \(x\in\left[-\frac{1}{4},+\infty \right)\).
Napisz równanie stycznej do wykresu funkcji \(f\) w punkcie \(x_0=2\). Zapisz obliczenia.
Funkcja \(f\) jest określona wzorem \(f(x)=x^4-2x^3+x^2-1\) dla każdej liczby rzeczywistej \(x \in [-1, 3]\).
Wyznacz zbiór wartości funkcji \(f\).
Trójkąt \(ABC\), w którym \(|AC| = |BC|\), jest wpisany w okrąg o promieniu \(R\). Środek tego okręgu leży wewnątrz trójkąta \(ABC\). Niech \(x\) oznacza odległość środka okręgu od podstawy \(AB\).
Wykaż, że pole trójkąta \(ABC\) jako funkcja zmiennej \(x\) jest określone wzorem \(P(x)=(R+x)\sqrt{R^2-x^2}\). Określ dziedzinę tej funkcji.
Dany jest okrąg o promieniu \(R\). Rozważamy wszystkie trójkąty spełniające warunki:
- są wpisane w ten okrąg
- mają obwody równe 3R
- mają jeden z boków dwukrotnie dłuższy od drugiego.
Znajdź trójkąt o możliwie największym polu przy zadanych warunkach. Oblicz jego pole. Zapisz obliczenia.
Grażyna planuje zrobienie pudełka (bez wieczka) w kształcie prostopadłościanu. W tym celu zamierza wykorzystać prostokątny kawałek tektury o wymiarach \(10 \text{ cm} \times 16 \text{ cm}\), odcinając z każdego rogu kwadrat o boku \(x\) cm (zobacz rysunek). 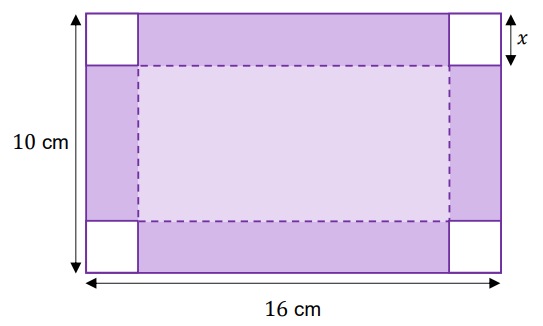

Oblicz wartość \(x\), dla której objętość otrzymanego pudełka będzie największa. Oblicz tę największą objętość pudełka. Zapisz obliczenia.
Dom \(D\) stoi w odległości \(5\) km od prostoliniowego odcinka drogi. W chwili początkowej Janusz znajduje się na tej drodze w punkcie \(A\) oddalonym od domu \(D\) o \(13\) km (zobacz rysunek). Janusz może iść drogą z maksymalną prędkością \(5\) km/h, zaś poza nią może poruszać się z maksymalną prędkością \(3\) km/h. 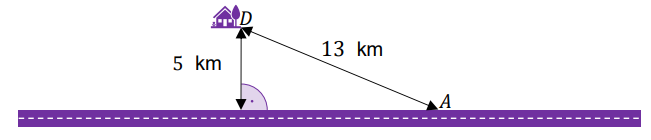

Oblicz najkrótszy czas potrzebny Januszowi na dojście do domu \(D\). Zapisz obliczenia.
Ciężarówka ma do pokonania trasę długości \(S\) km, poruszając się po autostradzie ze stałą prędkością \(v\) km/h. Minimalna prędkość dla ciężarówek na autostradzie wynosi \(40\) km/h, maksymalna - \(80\) km/h. Wiemy, że litr paliwa kosztuje \(8\) złotych, a kierowca otrzymuje \(42\) złote za godzinę swej pracy. Zużycie paliwa w ciągu jednej godziny jazdy autostradą w zależności od prędkości \(v\) wyrażone w litrach można opisać funkcją \(f(v)=7+\frac{v^2}{400}\).
Oblicz, przy jakiej prędkości koszt przejazdu będzie najmniejszy. Zapisz obliczenia.
Wskazówka: przyjmij, że koszt przejazdu jest sumą kosztu paliwa oraz wynagrodzenia kierowcy.
Dana jest kula o promieniu \(1\). Rozpatrujemy wszystkie stożki zawierające środek kuli i wpisane w tę kulę, to znaczy takie, w których: 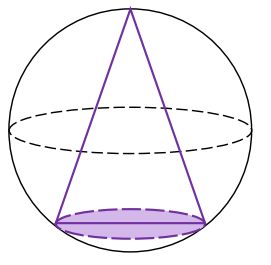
- wierzchołek leży na powierzchni kuli
- okrąg, będący krawędzią podstawy stożka, leży na powierzchni kuli (zobacz rysunek).

Oblicz promień podstawy tego stożka, który ma największą objętość. Oblicz objętość tego stożka. Zapisz obliczenia.
Dana jest kula o promieniu \(1\). Rozpatrujemy wszystkie stożki opisane na tej kuli, to znaczy takie, których: 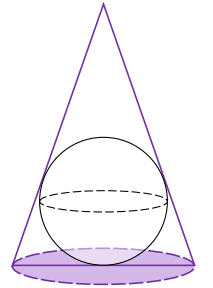
- podstawa ma dokładnie jeden punkt wspólny z kulą
- każda tworząca ma dokładnie jeden punkt wspólny z kulą (zobacz rysunek).

Wykaż, że objętość \(V\) stożka o wysokości \(h\) wyraża się wzorem \[V(h)=\frac{h^2\pi}{3(h-2)}\]
Oblicz wysokość tego stożka, który ma najmniejszą objętość. Oblicz objętość tego stożka. Zapisz obliczenia.
Wskazówka: skorzystaj z informacji, że objętość stożka o wysokości \(h\) wyraża się wzorem \[V(h)=\frac{h^2\pi}{3(h-2)}\]