Zestaw treningowy 2

Liczba \(2^{20}\cdot 4^{40}\) jest równa

A.\( 2^{60} \)

B.\( 4^{50} \)

C.\( 8^{60} \)

D.\( 8^{800} \)

Zbiór rozwiązań nierówności \(|x - 3| \ge 1\) jest przedstawiony na rysunku

O zdarzeniach losowych \(A\), \(B\) wiadomo, że: \(P(A) = 0{,}5\), \(P(B) = 0{,}3\) i \(P(A\cup B) = 0{,}7\). Prawdopodobieństwo iloczynu zdarzeń \(A\) i \(B\) spełnia warunek

A.\( P(A\cap B)=0{,}2 \)

B.\( P(A\cap B))>0{,}3 \)

C.\( P(A\cap B))\lt 0{,}2 \)

D.\( P(A\cap B))=0{,}3 \)

Wskaż liczbę, której \(6\%\) jest równe \(6\).

A.\( 0{,}36 \)

B.\( 3{,}6 \)

C.\( 10 \)

D.\( 100 \)

Różnica miar dwóch sąsiednich kątów wewnętrznych równoległoboku jest równa \(30^\circ\). Kąt rozwarty tego równoległoboku jest równy

A.\( 105^\circ \)

B.\( 115^\circ \)

C.\( 125^\circ \)

D.\( 135^\circ \)

Funkcja \(f\) jest określona wzorem \( f(x)=\begin{cases} {x-4\ \ \ \quad \text{ dla } x\le 3}\\ {-x+2\quad \text{ dla }x>3} \end{cases} \). Ile miejsc zerowych ma ta funkcja?

A.\( 0 \)

B.\( 1 \)

C.\( 2 \)

D.\( 3 \)

Kąt \(\alpha \) jest ostry i \(\sin\alpha = 0{,}75\). Wówczas

A.\( \alpha \lt 30^\circ \)

B.\( \alpha =30^\circ \)

C.\( \alpha =45^\circ \)

D.\( \alpha >45^\circ \)

Liczba \(7^{\frac{4}{3}}\cdot \sqrt[3]{7^5}\) jest równa

A.\( 7^{\frac{4}{5}} \)

B.\( 7^3 \)

C.\( 7^{\frac{20}{9}} \)

D.\( 7^2 \)

Dana jest funkcja \(y = f(x)\) określona dla \(x\in \langle -1, 8 \rangle\), której wykres jest przedstawiony na rysunku.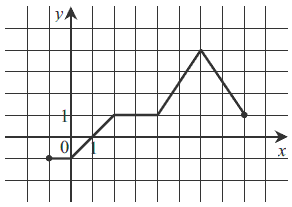

Wskaż zbiór wartości tej funkcji

A.\( \{-1,0,1,2,3,4,5,6,7,8\} \)

B.\( (-1,4) \)

C.\( \langle -1,4 \rangle \)

D.\( \langle -1,8 \rangle \)

Trzeci wyraz ciągu geometrycznego jest równy \(4\), a piąty wyraz tego ciągu jest równy \(1\). Pierwszy wyraz tego ciągu jest równy

A.\( 4 \)

B.\( 4\sqrt{2} \)

C.\( 16 \)

D.\( 16\sqrt{2} \)

Pewien wielościan ma \(6\) krawędzi. Liczba jego ścian jest równa

A.\( 4 \)

B.\( 5 \)

C.\( 6 \)

D.\( 9 \)

Wykres funkcji kwadratowej \(f(x) = (x - 3)^2 - 2\) nie ma punktów wspólnych z prostą o równaniu

A.\( y=-3 \)

B.\( y=-1 \)

C.\( y=1 \)

D.\( y=3 \)

Odcinki \(AB\) i \(CD\) są równoległe. Długości odcinków \(AB\), \(CD\) i \(AD\) są podane na rysunku. Długość odcinka \(DE\) jest równa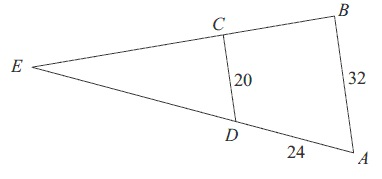

A.\( 44 \)

B.\( 40 \)

C.\( 36 \)

D.\( 15 \)

Wskaż równanie okręgu o środku \(S = (1,- 2)\) i promieniu \(r = 2\)

A.\( (x-1)^2+(y+2)^2=2 \)

B.\( (x+1)^2+(y-2)^2=2 \)

C.\( (x-1)^2+(y+2)^2=4 \)

D.\( (x+1)^2+(y-2)^2=4 \)

Równanie \(\frac{2x+1}{x}=3x\)

A.ma dwa rozwiązania: \( x=-\frac{1}{3}, x=1 \).

B.ma dwa rozwiązania: \( x=\frac{1}{3}, x=1 \).

C.nie ma żadnego rozwiązania.

D.ma tylko jedno rozwiązanie: \( x=1 \)

Suma długości wszystkich krawędzi sześcianu jest równa \(24\). Objętość tego sześcianu jest równa

A.\( 64 \)

B.\( 27 \)

C.\( 24 \)

D.\( 8 \)

Ciąg \((a_n)\) jest określony wzorem \(a_n = (-1)^n\cdot (n^2 - 2n)\) dla \(n \ge 1\). Wtedy

A.\( a_3>3 \)

B.\( a_3=3 \)

C.\( a_3\lt 2 \)

D.\( a_3=2 \)

Liczba \(\log 12\) jest równa

A.\( \log 3\cdot \log 4 \)

B.\( \log 3+ \log 4 \)

C.\( \log 16-\log 4 \)

D.\( \log 10+\log 2 \)

Zbiorem rozwiązań nierówności \(x^2 > 4x\) jest

A.\( (-\infty ,-4)\cup (0,+\infty ) \)

B.\( (4,+\infty ) \)

C.\( (-\infty ,-2)\cup (2,+\infty ) \)

D.\( (-\infty ,0)\cup (4,+\infty ) \)

Prosta \(l\) ma równanie \(y = -7x + 2\). Równanie prostej prostopadłej do \(l\) i przechodzącej przez punkt \(P = (0, 1)\) ma postać

A.\( y=7x-1 \)

B.\( y=7x+1 \)

C.\( y=\frac{1}{7}x+1 \)

D.\( y=\frac{1}{7}x-1 \)