Dany jest prostokąt \(ABCD\). Na boku \(CD\) tego prostokąta wybrano taki punkt \(E\), że \(|EC|=2|DE|\), a na boku \(AB\) wybrano taki punkt \(F\), że \(|BF|=|DE|\). Niech \(P\) oznacza punkt przecięcia prostej \(EF\) z prostą \(BC\) (zobacz rysunek). Wykaż, że trójkąty \(AED\) i \(FPB\) są przystające. 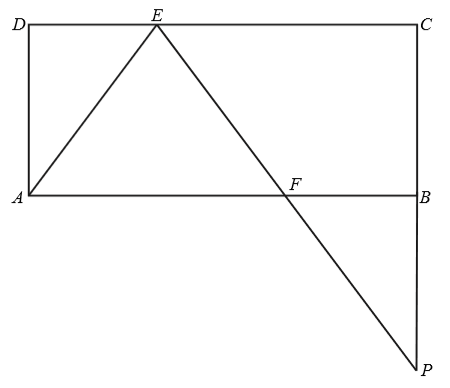

Strony z tym zadaniem
Matura 2018 czerwiecSąsiednie zadania
Zadanie 2682Zadanie 2683Zadanie 2684 (tu jesteś)
Zadanie 2685Zadanie 2686