Odcinek \(AB\) jest średnicą okręgu o środku \(O\) i promieniu \(r\). Na tym okręgu wybrano punkt \(C\), taki, że \(|OB|=|BC|\) (zobacz rysunek). 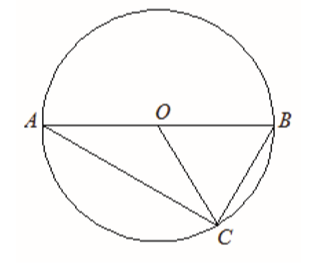 Pole trójkąta \(AOC\) jest równe
Pole trójkąta \(AOC\) jest równe
 Pole trójkąta \(AOC\) jest równe
Pole trójkąta \(AOC\) jest równe A.\( \frac{1}{2}r^2 \)
B.\( \frac{1}{4}r^2 \)
C.\( \frac{\pi}{4}r^2 \)
D.\( \frac{\sqrt{3}}{4}r^2 \)
Strony z tym zadaniem
Matura 2018 czerwiecSąsiednie zadania
Zadanie 2669Zadanie 2670Zadanie 2671 (tu jesteś)
Zadanie 2672Zadanie 2673